В механике все силы делятся на две группы: консервативные и неконсервативные.
Полная механическая энергия — это сумма потенциальной и кинетической энергии тела в определенный момент времени:
E = Ek + Ep
Закон сохранения механической энергии
В замкнутой системе, в которой действуют консервативные силы, механическая энергия сохраняется.
E = const
Согласно закону сохранения энергии, сумма потенциальной и кинетической энергии системы до взаимодействия тел равна сумме потенциальной и кинетической энергий системы после их взаимодействия:
Ek0 + Ep0 = Ek + Ep
Закон сохранения механической энергии для движения в поле тяжести Земли
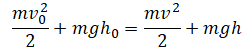
Примеры определения полной механической энергии в начальном и конечном положении
| Пример | Полная механическая энергия в начальной точке (А) | Полная механическая энергия в конечной точке (В) |
|
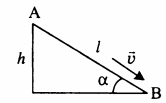
Спуск по наклонной плоскости из состояния покоя
|
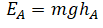
Высоту, на которой изначально находилось тело, можно рассчитать по формуле:
|
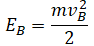 |
|
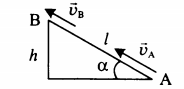
Подъем по наклонной плоскости
|
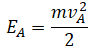 |
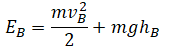
Высоту, на которую поднялось тело, можно рассчитать по формуле:
|
|
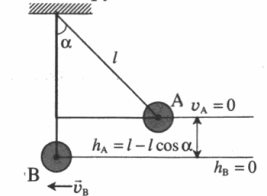
Груз на нити
|
Высоту, на которой изначально находилось тело, можно рассчитать по формуле:
|
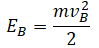 |
|
Вертикальный выстрел из пружинного пистолета |
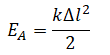 |
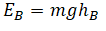 |
Пример №1. Камень брошен вертикально вверх. В момент броска он имел кинетическую энергию, равную 30 Дж. Какую потенциальную энергию относительно поверхности земли будет иметь камень в верхней точке траектории полета? Сопротивлением воздуха пренебречь.
Так как это условно замкнутая система (сопротивлением воздуха мы пренебрегаем), мы можем применить закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Учтем, что в момент броска камень находился на поверхности земли. Поэтому он обладал максимальной кинетической энергией и нулевой потенциальной. Но в верхней точке траектории его скорость стала равна нулю. Поэтому его кинетическая энергия тоже стала равна нулю. Зато потенциальная энергия в этой точке возросла до максимума. Поэтому:
Ek0 + 0 = 0 + Ep
Ek0 = Ep
Следовательно, потенциальная энергия в верхней точки траектории полета равна 30 Дж.
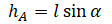
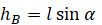
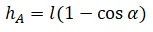
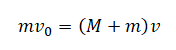
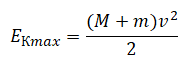
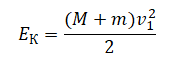
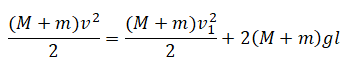
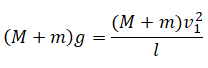
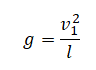
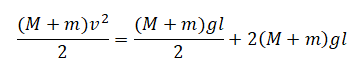
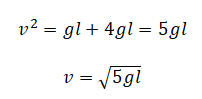
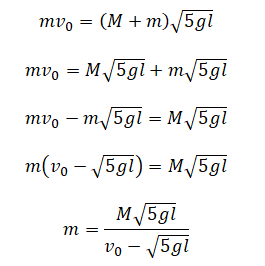
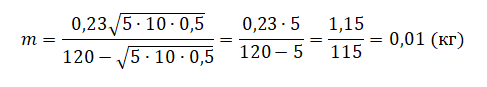
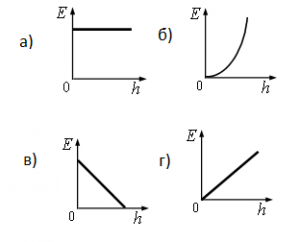 Какой из графиков, приведённых на рисунке, показывает зависимость полной энергии Е тела, брошенного под углом к горизонту, от его высоты h над Землёй? Сопротивлением воздуха пренебречь.
Какой из графиков, приведённых на рисунке, показывает зависимость полной энергии Е тела, брошенного под углом к горизонту, от его высоты h над Землёй? Сопротивлением воздуха пренебречь.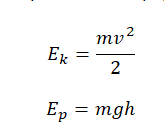
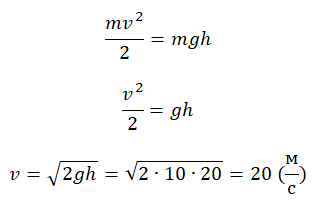
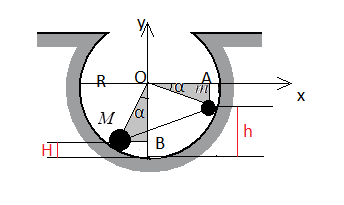
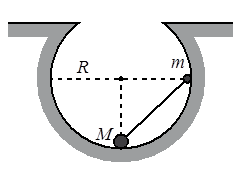 Небольшие шарики, массы которых m = 30 г и M = 60 г, соединены лёгким стержнем и помещены в гладкую сферическую выемку.
Небольшие шарики, массы которых m = 30 г и M = 60 г, соединены лёгким стержнем и помещены в гладкую сферическую выемку.