Принцип суперпозиции магнитных полей 🐲 СПАДИЛО.РУ

Если в некоторой точке пространства накладываются магнитные поля, то результирующий вектор магнитной индукции находят как геометрическую сумму вектором магнитной индукции, составляющих магнитное поле:

$\to B = \sum {\to B}_{i}$

Частные случаи принципа суперпозиции полей

Сложение векторов магнитной индукции, направленных вдоль одной прямой
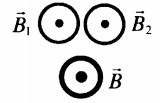	Если ${\to B}_{1} ↑ ⏐ ⏐ ↑ ⏐ ⏐ {\to B}_{2}$ , то: $B = B_{1} + B_{2}$
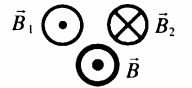	Если ${\to B}_{1} ↑ ⏐ ⏐ ⏐ ⏐ ↓ {\to B}_{2}$ , то: $B = \| B_{1} - B_{2} \|$
Сложение векторов магнитной индукции, перпендикулярных друг другу
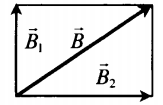	Если ${\to B}_{1} ⊥ {\to B}_{2}$ , то применяется теорема Пифагора: $B = \sqrt{{B_{1}}_{1}^{2} + {B_{2}}_{2}^{2}}$
Сложение векторов магнитной индукции, расположенных под углом друг другу
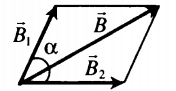	В этом случае применяется теорема косинусов: $B = \sqrt{{B_{1}}_{1}^{2} + {B_{2}}_{2}^{2} - 2 B_{1} B_{2} cos . (180 ° - α)}$

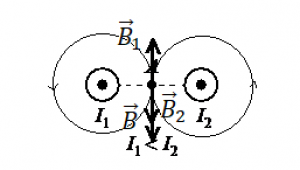
Пример №1. По двум тонким прямым проводникам, параллельным друг другу, текут одинаковые токи I (см. рисунок). Как направлено (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) создаваемое ими магнитное поле в точке С?

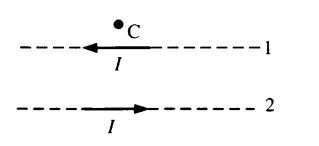
Чтобы определить направление результирующего вектора магнитной индукции, сначала определим направление линий магнитной индукции в точке С для каждого из полей. Применив правило буравчика, получим, что силовые линии первого поля направлены в точке С от нас, а второго поля — к нам. Но точка С находится на разных расстояниях от проводников. Она ближе к проводнику 1. Поскольку магнитное поле ослабевает с увеличением расстояния, то модуль вектора магнитной индукции первого поля в точке С будет больше вектора магнитной индукции второго поля. Поскольку они не компенсируют друг друга, и первое поле в этой точке сильнее второго, то результирующий вектор магнитной индукции в точке С направлен в сторону от наблюдателя.

Задание EF22750

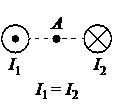На рисунке показаны сечения двух параллельных прямых длинных проводников и направления токов в них. Сила тока в проводниках одинакова. Куда направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор индукции созданного проводниками магнитного поля в точке А, расположенной на равном расстоянии от проводников? Ответ запишите словом (словами).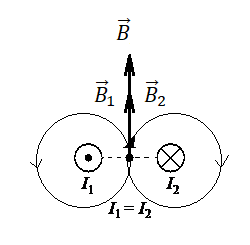

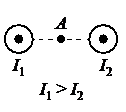Алгоритм решения

1.Определить направление вектора магнитной индукции в точке А для первого проводника с током.

2.Определить направление вектора магнитной индукции в точке А для второго проводника с током.

3.Установить направление результирующего вектора магнитной индукции.

Решение

Направление вектора магнитной индукции в точке А для обоих проводников можно определить с помощью правила буравчика. Мысленно направим буравчик по направлению тока в первом проводнике. Тогда получим, что силовые линии магнитного поля направлены против хода часовой стрелки. Поэтому вектор ${\to B}_{1}$ магнитной индукции в точке А направлен относительно рисунка вверх.

Поскольку во втором проводнике направление тока противоположно направлено току в первом проводнике, силовые линии создаваемого им магнитного поля направлены по ходу часовой стрелки. Но так как точка А относительно этого проводника расположена не справа, а слева, то вектор ${\to B}_{2}$ магнитной индукции в ней тоже направлен вверх.

Поскольку сила тока в обоих проводниках одинаковая, результирующий вектор магнитной индукции в точке А равен удвоенному вектору магнитной индукции поля, создаваемого каждым из этих проводников. В этом случае он направлен вверх так же как векторы ${\to B}_{1}$ и ${\to B}_{2}$ .

Ответ: Вверх

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF19061

На рисунке показаны сечения двух параллельных длинных прямых проводников и направления токов в них. Сила тока I₁ в первом проводнике больше силы тока I₂ во втором. Куда направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор индукции магнитного поля этих проводников в точке А, расположенной точно посередине между проводниками? Ответ запишите словом (словами).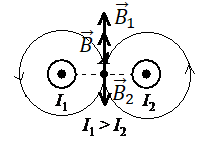

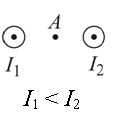Алгоритм решения

1.Определить направление вектора магнитной индукции в точке А для первого проводника с током.

2.Определить направление вектора магнитной индукции в точке А для второго проводника с током.

3.Установить направление результирующего вектора магнитной индукции.

Решение

Поскольку во втором проводнике направление тока совпадает с направлением тока в первом проводнике, силовые линии создаваемого им магнитного поля тоже направлены против хода часовой стрелки. Но так как точка А относительно этого проводника расположена не справа, а слева, то вектор ${\to B}_{2}$ магнитной индукции в ней направлен вниз.

Поскольку сила тока в первом проводнике больше, он создает более сильное магнитное поле. Следовательно, модуль вектора ${\to B}_{1}$ магнитной индукции больше модуля вектора ${\to B}_{2}$ . Тогда вектор, являющийся их геометрической суммой, будет направлен вверх.

Ответ: Вверх

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18500

На рисунке показаны сечения двух параллельных длинных прямых проводников и направления токов в них. Как направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор магнитной индукции в точке А, находящейся точно посередине между проводниками, если сила тока I₂ во втором проводнике больше силы тока I₁ в первом проводнике? Ответ запишите словом (словами).

Алгоритм решения

1.Определить направление вектора магнитной индукции в точке А для первого проводника с током.

2.Определить направление вектора магнитной индукции в точке А для второго проводника с током.

3.Установить направление результирующего вектора магнитной индукции.

Решение

Поскольку во втором проводнике направление тока совпадает с направлением тока в первом проводнике, силовые линии создаваемого им магнитного поля тоже направлены против хода часов стрелки. Но так как точка А относительно этого проводника расположена не справа, а слева, то вектор ${\to B}_{2}$ магнитной индукции в ней направлен вниз.

Поскольку сила тока во втором проводнике больше, он создает более сильное магнитное поле. Следовательно, модуль вектора ${\to B}_{2}$ магнитной индукции больше модуля вектора ${\to B}_{1}$ . Тогда вектор, являющийся их геометрической суммой, будет направлен вниз.

Ответ: Вниз

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | 📄 Скачать PDF | Просмотров: 513 | Оценить:

Принцип суперпозиции магнитных полей

теория по физике 🧲 магнетизм

Частные случаи принципа суперпозиции полей

Добавить комментарий Отменить ответ