Опишем колебания, которые происходят в цепи переменного тока при включении в нее конденсатора и катушки индуктивности. А также рассмотрим условия, при выполнении которых в цепи переменного тока наступает резонанс. Получим формулы для вычисления амплитуд напряжений, введем понятия емкостного и индуктивного сопротивления и выясним, какую роль играют эти величины.
Конденсатор в цепи переменного тока
Постоянный ток не может существовать в цепи, содержащий конденсатор. Движению электронов препятствует диэлектрик, расположенный между обкладками. Но переменный ток в такой цепи существовать может, что доказывает опыт с лампой (см. рисунок ниже).
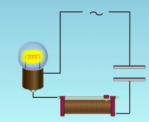
Пусть фактически такая цепь разомкнута, но если по ней течет переменный ток, конденсатор то заряжается, то разряжается. Ток, текущий при перезарядке конденсатора нагревает нить лампы, и она начинает светиться.
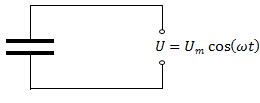
Найдем, как меняется сила тока в цепи, содержащей только конденсатор, если сопротивление проводов и обкладок конденсатора можно пренебречь (см. рис. выше). Напряжение на конденсаторе будет равно:
u=φ1−φ2=qC
Учтем, что напряжение на конденсаторе равно напряжению на концах цепи:
qC=Umaxcosωt
Следовательно, заряд конденсатора меняется по гармоническому закону:
q=CUmaxcosωt
Тогда сила тока, представляющая собой производную заряда по времени, будет равна:
i=q´=−CUmaxsinωt=CUmaxcos(ωt+π2)
Следовательно, колебания силы тока опережают колебания напряжения на конденсаторе на π2 (см. график ниже). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того, как напряжение достигнет максимума, сила тока становится равной нулю и т.д.
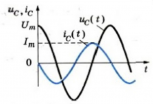
Амплитуда силы тока равна:
Imax=UmaxCω
Примем, что:
1Cω=XC
Также будем использовать действующие значения силы тока и напряжения. Тогда получим, что:
Обратите внимание, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода (при разрядке конденсатора), эта энергия возвращается в сеть.
Пример №1. Максимальный заряд на обкладках конденсатора колебательного контура qmax=10−6 Кл. Амплитудное значение силы тока в контуре Imax=10−3 А. Определите период колебания (потерями на нагревание проводника пренебречь).
Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значения магнитного поля катушки:
q2max2C=LI2max2
Отсюда:
LC=q2maxI2max
√LC=qmaxImax
T=2π√LC=2πqmaxImax=2·3,1410−610−3≈6,3·10−3 (с)
Катушка индуктивности в цепи переменного тока
Соберем две электрических цепи, состоящих из лампы накаливания, катушки индуктивности и источника питания: в первом случае постоянного, во втором — переменного (см. рисунки «а» и «б» ниже).
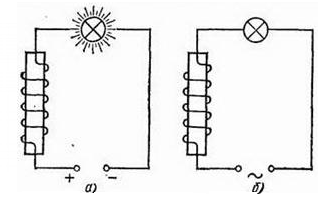
Опыт покажет, что в цепи постоянного тока лампа светится ярче по сравнению с той, что включена в цепь переменного тока. Это говорит о том, что сила тока в цепи постоянного тока выше действующего значения силы тока в цепи переменного тока.
Результат опыта легко объясняется явлением самоиндукции. При подключении катушки к постоянному источнику тока сила тока нарастает постепенно. Возрастающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь спустя какое-то время сила тока достигает наибольшего значения, соответствующему данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не успевает достигнуть максимального значения. Поэтому максимальное значение силы тока в цепи переменного тока с катушкой индуктивности ограничивается индуктивность. Чем больше индуктивность и чем больше частота приложенного напряжения, тем меньше амплитуда силы переменного тока.
Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (см. рисунок ниже). Для этого найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.
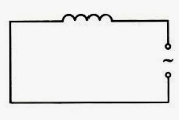
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна равняться нулю. Иначе, согласно закону Ома, сила тока была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля →Ei, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля →Eк, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства →Ei=−→Eк следует, что удельная работа вихревого поля (т.е. ЭДС самоиндукции ei) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Учитывая, что удельная работа кулоновского поля равна напряжения на концах катушки, можно записать:
ei=−u
Напомним, что сила переменного тока изменяется по гармоническому закону:
i=Imaxsinωt
Тогда ЭДС самоиндукции равна:
ei=−Li´=−LωImaxcosωt
Так как u=−ei, то напряжение на концах катушки оказывается равным:
u= LωImaxcosωt=LωImaxsin(ωt+π2)=Umax(ωt+π2)
Амплитуда напряжения равна:
Umax=LωImax
Следовательно, колебания напряжения на катушке опережают колебания силы тока на π2, или колебания силы тока отстают от колебаний напряжения на π2, что одно и то же.
В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (см. график ниже).

Но в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Амплитуда силы тока в катушке равна:
Imax=UmaxLω
Введем обозначение:
Lω=XL
Также будем использовать вместо амплитуд действующие значения силы тока и напряжения. Тогда получим:
Пример №2. Катушка с индуктивным сопротивлениемXL=500 Ом присоединена к источнику переменного напряжения, частота которого ν = 1000 Гц. Действующее значение напряжения U = 100 В. Определите амплитуду силы тока Imax в цепи и индуктивность катушки L. Активным сопротивлением пренебречь.
Индуктивное сопротивление катушки выражается формулой:
XL=Lω=2πνL
Отсюда:
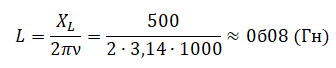
Так как амплитуда напряжения связана с его действующим значением соотношением Umax=U√2, то для амплитуды силы тока получаем:
Резонанс в электрической цепи
Механические и электромагнитные колебания имеют разную природу, но процессы, происходящие при этом, идентичны. Поэтому можно предположить, что резонанс в электрической цепи так же реален, как резонанс в колебательной системе, на которую действует периодическая сила.
Напомним, что в механической системе резонанс тем более заметен, чем меньше в колебательной системе трение между ее элементами. Роль трения в электрической цепи играет активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока во внутреннюю энергию проводника, который при этом нагревается. Следовательно, резонанс в электрической цепи будет отчетливо наблюдаться при малом активном сопротивлении R.
Если активное сопротивление мало, то собственная частота колебаний в колебательном контуре определяется формулой:
ω0=1√LC
Сила тока при вынужденных колебаниях должна достигать максимальных значений, когда частота переменного напряжения, приложенного к контуру равна собственной частоте колебательного контура:
ω=ω0=1√LC
После включения внешнего переменного напряжения резонансное значение силы тока в цепи устанавливается не моментально, а постепенно. Амплитуда колебаний силы тока возрастает до тех пор, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:
I2maxR2=UmaxImax2
Упростив это уравнение, получим:
ImaxR=Umax
Следовательно, амплитуда установившихся колебаний силы тока при резонансе определяется уравнением:
Imax=UmaxR
При сопротивлении, стремящемся к нулю, сила тока возрастает до бесконечно больших значений. При большом сопротивлении сила тока возрастает незначительно. Это хорошо видно на графике ниже.
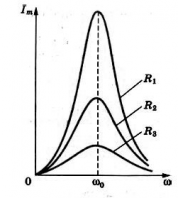
Пример №3. В цепь переменного тока с частотой ν = 500 Гц включена катушка индуктивностью L = 10 мГн. Какой емкости конденсатор надо включить в эту цепь, чтобы наступил резонанс?
Электрическая цепь, описываемая в условии, представляет собой колебательный контур. Резонанс в этой цепи наступит, когда частота переменного тока будет равна собственной частоте колебательного контура (ν = ν0).
Но:
ν0=12π√LC
Тогда:
ν=12π√LC
Отсюда:
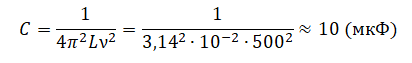
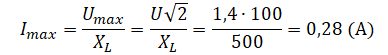
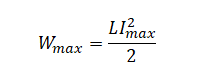
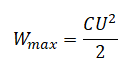
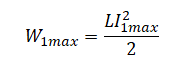
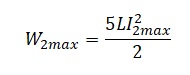
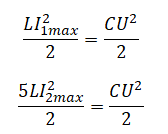
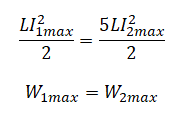
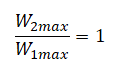
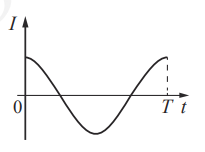 На рисунке приведён график зависимости силы тока от времени в катушке индуктивности идеального колебательного контура. Графики А и Б представляют изменения физических величин, характеризующих колебания в контуре. Установите соответствие между графиками и физическими величинами, зависимость которых от времени эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
На рисунке приведён график зависимости силы тока от времени в катушке индуктивности идеального колебательного контура. Графики А и Б представляют изменения физических величин, характеризующих колебания в контуре. Установите соответствие между графиками и физическими величинами, зависимость которых от времени эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

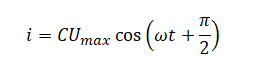
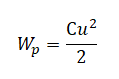
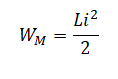
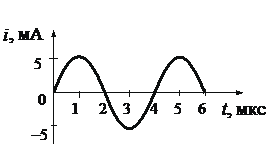 На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.
На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.