Легче всего решать задачу, если все приложенные к телу силы параллельны — тогда можно получить ответ, используя лишь правило моментов. Если же силы непараллельные, то иногда для получения ответа требуется дополнительно применять второй закон Ньютона.
Параллельные силы
Типовы задачи на правило моментов при параллельных силах
| Прямая неоднородная балка длиной l и массой m подвешена за концы на вертикально натянутых тросах. Балка занимает горизонтальное положение. Найдите силу натяжения первого троса T2, если центр тяжести балки находится на расстоянии a от левого конца балки. | 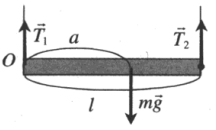
Для решения задачи в качестве положения оси вращения удобно выбрать точку приложения силы натяжения первого троса (потому что ее искать не нужно). Тогда плечом силы тяжести будет расстояние a, а плечом силы натяжения второго троса — l. Поэтому правило моментов можно записать так: T2l = mga T2 = mga/l |
| Рельс длиной l и массой m поднимают равномерно в горизонтальном положении на двух вертикальных тросах, первый из которых укреплен на конце рельса, а второй — на расстоянии x от другого конца. Определите натяжение второго троса. | 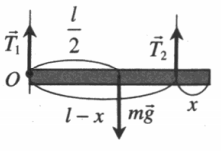
В этой задаче положение оси вращения также удобно выбрать в точке О, соответствующей точке приложения силы натяжения нити первого троса (так как ее искать не нужно). Тогда плечом силы натяжения второго троса будет служить разность длины рельса и расстояния x, а плечом силы тяжести — половина длины рельса. Поэтому правило моментов примет вид: mgl/2 = T2(l – x) T2 = mgl2(l−x) |
Пример №1. К левому концу невесомого стержня прикреплен груз массой 3 кг (см. рисунок). Стержень расположили на опоре, отстоящей от груза на 0,2 длины. Груз какой массы надо подвесить к правому концу, чтобы стержень находился в равновесии?
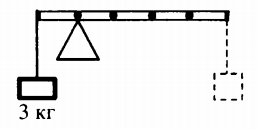
Условие равновесие будет выполняться, если произведение силы тяжести первого груза на ее плечо будет равно произведению силы тяжести второго груза на ее плечо:
Fтяж1d1 = Fтяж2d2
Согласно рисунку, второй груз будет подвешен на расстоянии 0,8 от опоры. Следовательно:
Fтяж2=Fтяж2d1d2=m1gd1d2
m2g=m1gd1d2
m2=m1d1d2=3·0,20,8=0,75 (кг)
Непараллельные силы
Типовы задачи на правило моментов при непараллельных силах
| Рабочий удерживает за один конец доску массой m так, что она образует угол α с горизонтом, опираясь о землю другим концом. С какой силой рабочий удерживает доску, если эта сила перпендикулярна доске? | 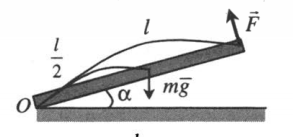
За точку равновесия примем точку касания доски с землей. Плечо силы тяжести будет равно нижнему катету треугольника, образованного при опускании перпендикуляра к земле из точки приложения этой силы: d1 = l cosα/2 Плечо силы, с которой рабочий поднимает доску, равно длине доски: d2 = l Отсюда: mglcosα2=Fl F=2lmglcosα=2mgcosα |
| В гладкий высокий цилиндрический стакан с внутренним радиусом R помещают карандаш длиной l и массой m. С какой силой действует на стакан верхний конец карандаша? | 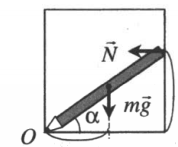
За точку равновесия примем нижнюю точку карандаша. Сила давления верхнего конца карандаша на стакан по модулю будет равна силе нормальной реакции опоры в этой точке. Поэтому плечо ее силы будет равно произведению длины карандаша на синус угла между ним и дном стакана: d1 = l sinα Минимальным расстоянием между линией действия силы тяжести и точкой равновесия будет половина произведения длины карандаша на косинус угла между ним и дном стакана: d2 = l сosα/2 Отсюда: Nl sinα = mgl сosα/2 N=mglcosα2lsinα Плечо силы тяжести также равно радиусу стакана, а плечо силы реакции опоры можно найти из теоремы Пифагора. Отсюда: N=mgR√l2−4R2 |
| Колесо радиусом R и массой m стоит перед ступенькой высотой h. Какую наименьшую горизонтальную силу надо приложить, чтобы оно могло подняться на ступеньку? Сила трения равна нулю. | 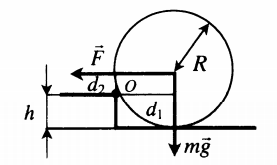
За точку равновесия примем точку касания колеса со ступенькой. Плечо силы тяжести является катетом треугольника, образованного с радиусом колеса и плечом прикладываемой силы. Плечо этой силы равно разности радиуса и высоты ступеньки. d1=√R2−d22 d2 = R – h Отсюда: mg√R2−d22=F(R−h) F=mg√R2−d22R−h=mg√h(2R−h)R−h |
| Лестница массой m приставлена к гладкой вертикальной стене пол углом α. Найдите силу давления лестницы на стену. Центр тяжести лестницы находится в ее середине. | 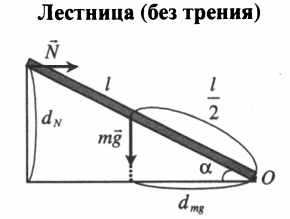
Плечо силы тяжести равно половине произведения длины лестницы на косинус угла α. Плечо силы реакции опоры равно произведению этой длины на синус α. Поэтому правило моментов записывается так: Nlsinα=mglcosα2 Отсюда: N=mglcosα2lsinα=mg2tanα |
| Лестница длиной l приставлена к идеально гладкой стене под углом α к горизонту. Коэффициент трения между лестницей и полом μ. На какое расстояние x вдоль лестницы может поднять человек, прежде чем лестница начнет скользить? Массой лестницы пренебречь. | 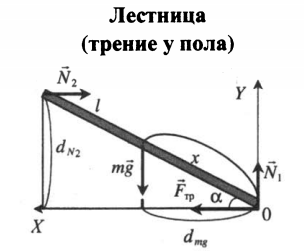
Правило моментов: mgxcosα=N2lsinα Второй закон Ньютона в проекциях на оси Ox и Oy соответственно: Fтр – N2 = 0 N1 – mg = 0 Сила трения: Fтр = μmg = N2 Следовательно: mgxcosα=μmglsinα x=μmglsinαmgxcosα=μltanα |
| Однородная лестница приставлена к стене. При каком наименьшем угле α между лестницей и горизонтальным полом лестница сохранит равновесие, если коэффициент трения между лестницей и полом μ1, а между лестницей и стеной — μ2? | 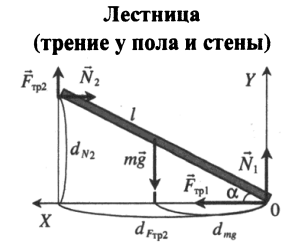
Правило моментов: mgl2cosα=Fтр2lcosα+N2lsinα Второй закон Ньютона в проекциях на ось Ox: Fтр1 – N2 = 0 μ1N1 – N2 = 0 На ось Oy: Fтр2 + N1 – mg = 0 μ2N2 +N2μ1 = mg N2(μ2+1μ1)=mg N2=mgμ2+1μ1=mgμ1μ1μ2+1 Fтр2=mg−N1=mg−N2μ1=mg−mgμ1μ2+1=mg(1−1μ1μ2+1) mgl2cosα=mg(1−1μ1μ2+1)lcosα+mgμ1μ1μ2+1lcosα Преобразуем выражение и получим: tanα=1−μ1μ21μ1 |
| Какую минимальную горизонтальную силу нужно приложить к верхнему ребру куба массой m, находящегося на горизонтальной плоскости, чтобы перекинуть его через нижнее ребро? | 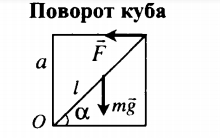
Правило моментов примет вид: mgl2cosα=Flsinα У куба угол α равен 45 градусам, а синус и косинус этого угла равны. Длины диагонали взаимоуничтожаются. Остается: F=mg2 |
Пример №2. Невесомый стержень длиной 1 м, находящийся в ящике с гладким дном и стенками, составляет угол α = 45о с вертикалью (см. рисунок). К стержню на расстоянии 25 см от его левого конца подвешен на нити шар массой 2 кг. Каков модуль силы N, действующий на стержень со стороны левой стенки ящика?
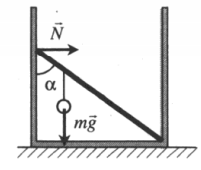
25 см = 0,25 м
Пусть точкой равновесия будет точка касания нижнего конца стержня с дном ящика. Тогда плечом силы тяжести будет:
d1 = (l – 0,25)sinα
Плечом силы реакции опоры будет:
d2 = l cosα
Запишем правило моментов:
mg(l−0,25)sinα=Nlcosα
Отсюда:
N=mg(l−0,25)sinαlcosα
Так как косинус и синус угла 45о равны, получим:
N=mg(l−0,25)l=2·10(1−0,25)1=15 (Н)
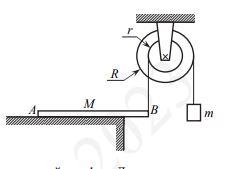 Однородный брусок AB массой M постоянного прямоугольного сечения лежит на гладкой горизонтальной поверхности стола, свешиваясь с него менее чем наполовину (см. рисунок). К правому концу бруска прикреплена лёгкая нерастяжимая нить. Другой конец нити закреплён на меньшем
из двух дисков идеального составного блока. На большем диске этого блока закреплена другая лёгкая
нерастяжимая нить, на которой висит груз массой m = 1 кг. Диски скреплены друг с другом, образуя единое целое. R = 10 см, r = 5 см. Сделайте рисунок с указанием сил, действующих на брусок M, блок и груз m. Найдите минимальное значение M, при котором система тел остаётся неподвижной. Обоснуйте применимость используемых законов к решению задачи.
Однородный брусок AB массой M постоянного прямоугольного сечения лежит на гладкой горизонтальной поверхности стола, свешиваясь с него менее чем наполовину (см. рисунок). К правому концу бруска прикреплена лёгкая нерастяжимая нить. Другой конец нити закреплён на меньшем
из двух дисков идеального составного блока. На большем диске этого блока закреплена другая лёгкая
нерастяжимая нить, на которой висит груз массой m = 1 кг. Диски скреплены друг с другом, образуя единое целое. R = 10 см, r = 5 см. Сделайте рисунок с указанием сил, действующих на брусок M, блок и груз m. Найдите минимальное значение M, при котором система тел остаётся неподвижной. Обоснуйте применимость используемых законов к решению задачи.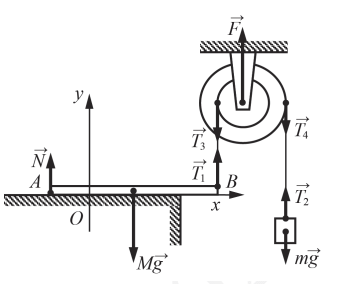
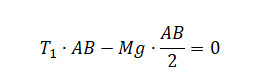
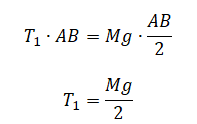
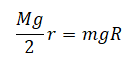
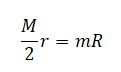
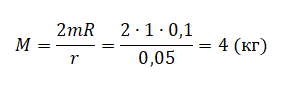
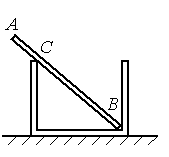 Однородный стержень АВ массой 100 г покоится, упираясь в стык дна и стенки банки концом В и опираясь на край банки в точке С (см. рисунок). Модуль силы, с которой стержень давит на стенку сосуда в точке С, равен 0,5 Н. Чему равен модуль горизонтальной составляющей силы, с которой стержень давит на сосуд в точке В, если модуль вертикальной составляющей этой силы равен 0,6 Н? Трением пренебречь.
Однородный стержень АВ массой 100 г покоится, упираясь в стык дна и стенки банки концом В и опираясь на край банки в точке С (см. рисунок). Модуль силы, с которой стержень давит на стенку сосуда в точке С, равен 0,5 Н. Чему равен модуль горизонтальной составляющей силы, с которой стержень давит на сосуд в точке В, если модуль вертикальной составляющей этой силы равен 0,6 Н? Трением пренебречь.
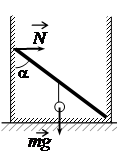 Невесомый стержень, находящийся в ящике с гладкими дном и стенками, составляет угол 45° с вертикалью (см. рисунок). К середине стержня подвешен на нити шарик массой 1 кг. Каков модуль силы упругости
Невесомый стержень, находящийся в ящике с гладкими дном и стенками, составляет угол 45° с вертикалью (см. рисунок). К середине стержня подвешен на нити шарик массой 1 кг. Каков модуль силы упругости
Всë хорошо и понятно!