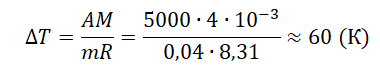Первое начало термодинамики | теория по физике 🧲 термодинамика

Первое начало термодинамики (первый закон термодинамики) представляет собой закон сохранения энергии в тепловых процессах.

Первое начало термодинамики

Внутренняя энергия идеального газа изменяется двумя способами: за счет теплопередачи или при совершении работы.

$\pm Δ U = \pm Q \pm A ‘$

Пояснение:

+∆U — внутренняя энергия газа увеличивается.
–∆U — внутренняя энергия газа уменьшается.
+Q — газ нагревают (газу передают количество теплоты).
–Q — газ охлаждается (газ отдает тепло окружающей среде).
+A’ — газ сжимает внешняя сила.
–A’ — газ расширяется, совершая работу.

Внимание! Знак перед работой показывает, как процесс совершения работы влияет на изменение внутренней энергии газа.

Пример №1. В некотором процессе внутренняя энергия газа уменьшилась на 300 Дж, а газ совершил работу 500 Дж. Какое количество теплоты было сообщено газу?

Чтобы рассчитать количество теплоты, сообщенное газу, нужно найти разность между изменением внутренней энергии и работой, совершенным газом. Для этого нужно правильно определить их знаки. Так как внутренняя энергия уменьшилась, она отрицательна. Но работа положительна. Поэтому газу было сообщено следующее количество теплоты:

Q = A – U = 500 – 300 = 200 (Дж)

Зависимость физических величин

Выясним, от чего зависят величины, входящие в формулу первого начала термодинамики. Изменение внутренней энергии идеального газа зависит от изменения температуры:

$Δ U = \frac{3}{2} ν R Δ T$

Работа идеального газа зависит от изменения его объема:

$A^{‘} = p Δ V$

Первое начало термодинамики для изопроцессов

Изотермический процесс (T = const)	$Δ U = 0, Q = A ‘$
Изохорный процесс (V = const)	$A^{‘} = 0, Δ U = Q$
Изобарное расширение газа (p = const)	$Δ U = Q - p Δ V$ $Δ U = Q - ν R Δ T$
Адиабатный (система не получает тепло извне и не отдает его окружающей среде, или Q = 0)	$Q = 0, Δ U = A ‘$

Пример №2. Идеальный одноатомный газ находится в сосуде с жесткими стенками объемом 0,6 куб. м. При нагревании его внутренняя энергия увеличилась на 18 кДж. На сколько возросло давление газа?

18 кДж = 18000 Дж

Внутреннюю энергию газа можно определить по формуле:

$Δ U = \frac{3}{2} ν R Δ T$

Отсюда изменение температуры равно:

$Δ T = \frac{2 Δ U}{3 ν R}$

Уравнение состояния идеального газа для 1 и 2 состояния:

$p_{1} V = ν R T_{1}$

$p_{2} V = ν R T_{2}$

Отсюда давления равны:

$p_{1} = \frac{ν R T_{1}}{V}$

$p_{2} = \frac{ν R T_{2}}{V}$

Разность давлений:

$p_{2} - p_{1} = \frac{ν R T_{2}}{V} - \frac{ν R T_{1}}{V} = \frac{ν R}{V} Δ T = \frac{ν R}{V} \cdot \frac{2 Δ U}{3 ν R} = \frac{2 Δ U}{3 V}$

$p_{2} - p_{1} = \frac{2 \cdot 18000}{3 \cdot 0, 6} = 20000 (П а) = 20 (к П а)$

Графические задачи на первое начало термодинамики

Рассмотрим графический способ решения задачи на первое начало термодинамики на конкретном примере.

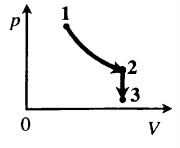
Задача: Один моль идеального одноатомного газа сначала изотермически расширился (T₁ = 300 К). Затем газ охладили, понизив давление в 3 раза (см. рисунок). Какое количество теплоты отдал газ на участке 2–3?

Порядок решения:

1. Определить температуры для всех указанных точек, учитывая графики процессов, масштаб и условие задачи.

T₁ = T₂ = 300 К; T₃ = 100 К

2. Определить, к какому изопроцессу относится тот участок графика, о котором спрашивают в задаче.

Участок 2–3 на графике — это изохорный процесс, так как давление остается постоянным.

3. Записать для него первое начало термодинамики.

В данном процессе:

$Δ U = Q$

4. Учитывая характер изменения величин, правильно расставить знаки: $- Δ U = - Q$ .

5. Подставляя в первое начало термодинамики формулы для расчета изменения внутренней энергии и работы газа, решить задачу.

Формула изменения внутренней энергии газа:

$Δ U = \frac{3}{2} ν R Δ T$

Формула работы газа:

$A^{‘} = p Δ V$

Так как процесс изохорный, работа газа равна нулю. Поэтому количество теплоты, отданное газом на участке 2–3, равно изменению внутренней энергии газа:

Изменение внутренней энергии равно:

$Q_{23} = \frac{3}{2} ν R Δ T_{23} = \frac{3}{2} \cdot 1 \cdot 8, 31 \cdot 200 = 2493 (Д ж)$

Текст: Алиса Никитина, 7.2k 👀

Задание ЕГЭ-Ф-ДВ2023-9

Газ получил количество теплоты, равное 300 Дж, при этом внутренняя энергия газа уменьшилась на 100 Дж. Масса газа не менялась. Какую работу совершил газ в этом процессе? Ответ запишите в Джоулях.

Алгоритм решения:

Записать исходные данные.
Записать формулу, отображающую зависимость между работой, внутренней энергией газа и количеством теплоты, полученным этим газом.
Подставить известные величины и сделать вычисления.

Решение:

Запишем исходные данные:

Количество теплоты, сообщенное газы: Q = 300 Дж.
Изменение внутренней энергии газа: ∆U = 100 Дж.

Зависимость между работой, внутренней энергией газа и количеством теплоты, полученным этим газом, устанавливает первое начало термодинамики:

–∆U = Q – A

Перед изменением внутренней энергией газа ставим знак «минус», так как в результате совершения описанного процесса внутренняя энергия газа уменьшилась. Перед количеством теплоты ставим знак «плюс», так как газу сообщили это количество теплоты. Перед работой ставим знак «минус», так как газ совершает ее. Следовательно, газ совершил работу:

A = Q + ∆U = 300 + 100 = 400 (Дж)

Ответ: 400

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17492

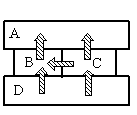Четыре металлических бруска положили вплотную друг к другу, как показано на рисунке. Стрелки указывают направление теплопередачи от бруска к бруску. Температуры брусков в данный момент 100°С, 80°С, 60°С, 40°С. Температуру 40°С имеет брусок

A
B
C
D

Алгоритм решения

Определить тип теплопередачи.
Вспомнить, как происходит этот тип теплопередачи.
Сделав анализ рисунка, установить, какой брусок имеет указанную в задаче температуру.

Решение

Так как это твердые тела, поверхности которых соприкасаются друг с другом, и перенос тепла происходит без переноса вещества, то этот вид теплопередачи является теплопроводностью. Тепло всегда направлено от более нагретого тела к менее нагретому.

На рисунке видно, что самым нагретым телом является нижний брусок, так как он только отдает тепло, но не принимает его. Средний брусок справа менее нагрет, чем нижний, так как принимает от него тепло. Но он более теплый по сравнению со средним бруском слева, так как он делится с ним теплом. И оба этих бруска отдают свою энергию верхнему бруску, который сам только принимает тепло, но не отдает его. Следовательно, именно он имеет температуру +40 ^оС.

Ответ: A

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17758

Один моль аргона, находящийся в цилиндре при температуре T₁=600 K и давлении p₁=4⋅10⁵ Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p₂=10⁵ Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?

Алгоритм решения

1.Записать исходные данные.

2.Записать уравнение состояния идеального газа.

3.Записать формулу для расчета внутренней энергии газа.

4.Используя первое начало термодинамики, выполнить общее решение задачи.

5.Подставив известные данные, вычислить неизвестную величину.

Решение

Запишем исходные данные:

• Начальная температура газа: T₁ = 600 К.

• Начальное давление: p₁ = 4∙10⁵ Па.

• Конечное давление: p₂ = 10⁵ Па.

• Работа, совершенная газом: A = 2493 Дж.

Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:

$p V = ν R T$

Внутренняя энергия одноатомного идеального газа пропорциональна температуре:

$U = \frac{3}{2} ν R T$

Внутренняя энергия аргона до расширения и после него:

$U_{1} = \frac{3}{2} ν R T_{1}$

$U_{2} = \frac{3}{2} ν R T_{2}$

Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:

$T = \frac{c o n s t}{V}$

$T_{1} V_{1} = T_{2} V_{2}$

Выразим конечную температуру:

$T_{2} = \frac{T_{1} V_{1}}{V_{2}}$

Составим уравнение состояния газа для состояний аргона 1 и 2:

$p_{1} V_{1} = ν R T_{1}$

$p_{2} V_{2} = ν R T_{2}$

Отсюда:

$ν R = \frac{p_{1} V_{1}}{T_{1}} = \frac{p_{2} V_{2}}{T_{2}}$

Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:

$\frac{V_{1}}{V_{2}} = \frac{p_{2} T_{1}}{p_{1} T_{2}}$

Подставим это отношение в формулу для конечной температуры:

$T_{2} = \frac{T_{1} V_{1}}{V_{2}} = \frac{p_{2} {T_{1}}_{1}^{2}}{p_{1} T_{2}}$

Отсюда:

$T_{2} = T_{1} \sqrt{\frac{p_{2}}{p_{1}}}$

Отсюда внутренняя энергия газа в состоянии 2 равна:

$U_{2} = \frac{3}{2} ν R T_{1} \sqrt{\frac{p_{2}}{p_{1}}}$

Уменьшение внутренней энергии аргона составило (изначально она была выше):

$Δ U = U_{1} - U_{2} = \frac{3}{2} ν R T_{1} - \frac{3}{2} ν R T_{1} \sqrt{\frac{p_{2}}{p_{1}}} = \frac{3}{2} ν R T_{1} (1 - \sqrt{\frac{p_{2}}{p_{1}}})$

В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:

$Δ U = Q + A$

Следовательно, газ отдал следующее количество теплоты:

$Q = Δ U - A = \frac{3}{2} ν R T_{1} (1 - \sqrt{\frac{p_{2}}{p_{1}}}) - A$

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17562

Газу передали изохорно количество теплоты 300 Дж. Как изменилась его внутренняя энергия в этом процессе?

Ответ:

а) увеличилась на 300 Дж

б) уменьшилась на 300 Дж

в) увеличилась на 600 Дж

г) уменьшилась на 600 Дж

Алгоритм решения

1.Записать исходные данные.

2.Записать первое начало термодинамики.

3.Установить, как меняется внутренняя энергия идеального газа.

Решение

Запишем исходные данные:

• Количество теплоты, переданное газу: Q = 300 Дж.

Первое начало термодинамики:

$Δ U = Q + A$

Так как по условию задачи это изохорный процесс, то работа равна 0. Следовательно, изменение внутренней энергии газа равно количеству теплоты:

$Δ U = Q = 300 (Д ж)$

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17597

Находясь в цилиндре двигателя, газ получил от нагревателя количество теплоты, равное 10 кДж. Затем он расширился, совершив работу 15 кДж. В результате всех этих процессов внутренняя энергия газа уменьшилась на

Ответ:

а) 5 кДж

б) 10 кДж

в) 15 кДж

г) 25 кДж

Алгоритм решения

1.Записать исходные данные.

2.Записать первое начало термодинамики.

3.Установить, как меняется внутренняя энергия идеального газа.

Решение

Запишем исходные данные:

• Количество теплоты, переданное газу: Q = 10 кДж.

• Работа, совершенная газом: A = 15 кДж.

Первое начало термодинамики:

$Δ U = Q + A$

В этой формуле за работу принимается та работа, что совершается над газом. Но в данном случае газ сам совершает работу. Поэтому первое начало термодинамики примет вид:

$Δ U = Q - A = 10 - 15 = - 5 (к Д ж)$

Знак «–» указывает на то, что внутренняя энергия газа уменьшилась на 5 кДж.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17579

При постоянном давлении гелий нагрели, в результате чего он совершил работу 5 кДж? Масса гелия 0,04 кг. Насколько увеличилась температура газа?

Ответ:

а) 60 К

б) 25 К

в) 15 К

г) 3 К

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Записать первое начало термодинамики.

3.Записать формулу для расчета работы газа.

4.Выполнить решение задачи в общем виде.

5.Подставить известные данные и выполнить вычисления искомой величины.

Решение

Запишем исходные данные:

• Газ совершил работу: A = 5 кДж.

• Масса гелия: m = 0,04 кг.

5 кДж = 5000 Дж

Первое начало термодинамики:

$Δ U = Q + A$

Учтем, что не над газом совершают работу, а сам газ совершает ее:

Отсюда:

$Δ U = Q - A$

Так как газ нагревали изобарно, часть тепла ушла на изменение внутренней энергии газа, а часть — на совершение этим газом работы.

Работа, совершенная газом, равна:

$A = p Δ V = \frac{m}{M} R Δ T$

Молярная масса гелия равна 4∙10^–3 кг/моль.

Отсюда:

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

ЕГЭ по физике

Вся теория

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

Зависимость физических величин

Первое начало термодинамики для изопроцессов

Графические задачи на первое начало термодинамики

Задание ЕГЭ-Ф-ДВ2023-9

Задание EF17492

Задание EF17758

Задание EF17562

Задание EF17597

Задание EF17579

ЕГЭ по физике

Вся теория

Добавить комментарий Отменить ответ