Отдельные частицы любого тела — твердого, жидкого или газообразного — взаимодействуют друг с другом. Поэтому если какая-то частица начинает колебаться, то благодаря взаимодействию между частицами это движение с некоторой скоростью начинает распространяться во все стороны.
В воздухе, твердых телах и внутри жидкостей механические волны возникают благодаря силам упругости. Эти силы осуществляют связь между отдельными частями тела. В образовании волн на поверхности воды играют роль сила тяжести и сила поверхностного натяжения. Такие волны позволяют наиболее наглядно рассмотреть главные особенности волнового движения.

Волна на поверхности воды представляет собой бегущие вперед валы округлой формы. Расстояние между валами, которые также называют гребнями, примерно одинаковы. Волны распространяются в среде с определенной скоростью. Так, если чайка летит вперед, а по ней в любой момент времени оказывается один и тот же гребень, то скорость распространения волны можно принять равной скорости полета чайки. Волны на воде наблюдать удобно потому, что скорость их распространения невелика.
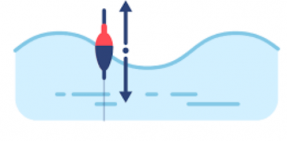
Если бросить в воду легкий предмет, он не будет увлекаться волной, а начнет совершать колебания вверх и вниз, оставаясь примерно на одном месте, как поплавок. Это говорит о том, что частицы воды остаются на месте в то время, как волна распространяется на большие расстояния.
Если же резко толкнуть горизонтальную пружину, можно будет наблюдать, как в одних местах она разрежается, в других — уплотняется. Это тоже волна. Видно, что энергия, полученная от толчка руки, переносится через пружину, хотя ее частицы остаются на месте.

Примеры с поплавком на воде и горизонтальной пружиной позволяют сделать вывод, что волна переносит энергию, но не переносит вещество среды.
Виды механических волн
По характеру колебаний частиц среды относительно положения равновесия различают два вида волн:
Волны, распространяющиеся вдоль резинового шнура, являются поперечными (см. рисунок ниже). Чтобы появилась волна, нужно взять конец шнура, прикрепленного к вертикальной опоре, и дернуть его. При этом волна побежит к вертикальной опоре, а сам шнур будет менять свою форму. Каждая частица шнура станет совершать колебания относительно своего неизмененного положения равновесия сверху вниз (перпендикулярно направлению распространения волны).
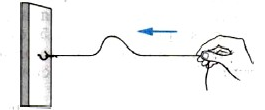
Рассмотрим поперечные волны подробнее. Каждый участок шнура обладает массой и упругостью. При деформации шнура в любом его сечении появляются силы упругости. Эти силы стремятся возвратить шнур в исходное положение. Благодаря инертности участок колеблющегося шнура не останавливается в положении равновесия, а проходит его, продолжая двигаться до тех пор, пока силы упругости не остановят этот участок в момент максимального отклонения от положения равновесия.
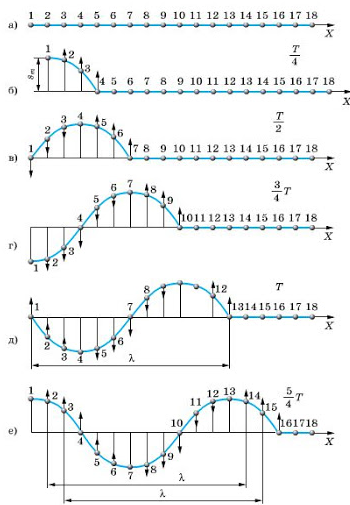
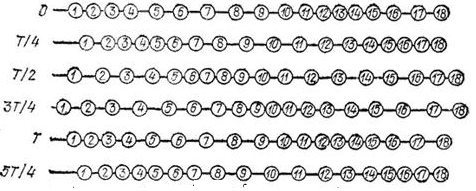
На рисунках а, б, в, г, д и е изображен процесс распространения поперечной волны. На них показаны положения частиц среды в последовательные моменты времени.
Теперь рассмотрим распространение в среде продольной волны. Такую волну можно наблюдать, собрав установку из цепочки массивных шариков, связанных пружинками. Шары подвешены так, чтобы они могли колебаться только вдоль цепочки (см. рисунок ниже).
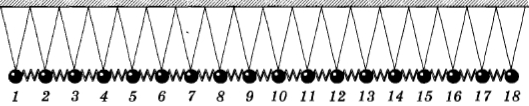
Если первый шар привести в колебательное движение, то вдоль цепочки побежит продольная волна, состоящая из чередующихся уплотнений и разрежений шаров. Уплотнения и разрежения (см. рисунок ниже) появляются вследствие горизонтальных колебаний шаров у положения равновесия. Волна также распространяется горизонтально.
Физические характеристики волны
Обратимся к рисункам д, е еще раз. Видно, что когда частица 1 находится в положении равновесия и движется вверх, частица 13 тоже находится в положении равновесия и движется вверх. Спустя четверть период частица 1 будет максимально отклонена от положения равновесия, ровно, как и частица 13. Так как частицы 1 и 13 движутся одинаково, говорят, что колебания этих частиц происходят в одинаковых фазах. Расстояние между этими частицами называют длиной волны.
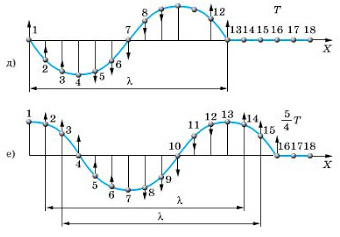
Внимание! В действительности частица 13 отстает по фазе от частицы 1 на 2π. Но поскольку такая разница фаз не приводит к различию в состояниях колеблющихся частиц, можно считать, что частицы колеблются в одинаковых фазах.
Длина волны обозначается как λ (лямбда). Единица измерения длины волны — метр (м).
Согласно рисунку е, в одинаковых фазах колеблются частицы 1 и 13, 2 и 14, 3 и 15, 4 и 16. Поэтому расстояния между этими частицами равно длине волны. Но частицы 1 и 7, находящиеся на расстоянии λ2, колеблются в противоположных фазах. Посмотрите на рисунок д: когда 1 частица находится в положении равновесия и движется вверх, частица 7 находится в положении равновесия и движется низ. На рисунке е обе частицы максимально отклонены от положения равновесия, но в противоположных направлениях.
Волна распространяется на расстояние λ за время, равное периоду колебаний частиц вещества. Зная расстояние, на которое распространилась волна, и время, в течение которого это распространение происходило, можно найти скорость волны:
v=λT
Но мы знаем, что период равен величине, обратной частоте колебаний:
T=1ν
Тогда скорость распространения волны равна:
При распространении волны мы имеем дело с периодичностью двоякого рода:
- Во-первых, каждая частица среды совершает периодические колебания во времени. В случае гармонических колебаний (эти колебания происходят по синусоидальному или косинусоидальному закону) частота постоянна и амплитуда одинакова во всех точках. Колебания отличаются только фазами.
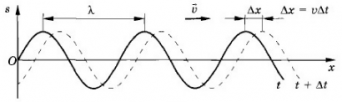
- Во-вторых, в данный момент времени форма волны повторяется в пространстве через отрезки длиной λ вдоль линии распространения волны. На рисунке ниже показан профиль волны в определенный момент времени (сплошная линия). С течением времени вся эта картина перемещается со скоростью v направо. Спустя промежуток времени ∆t волна будет иметь вид, изображенный на том же рисунке прерывистой линией.
Пример №1. Определите скорость распространение волны на поверхности воды, если расстояние между ее гребнями равно 1 метру. Учитывайте, что мимо наблюдателя за 5 секунд прошло 10 волн.
Обычно под волной на воде люди понимают гребни — частицы воды, максимально отклоненные от положения равновесия. Расстояние между гребнями равно длине волны. Чтобы найти скорость распространения волны, нужно знать частоту колебания молекул воды. Ее можно вычислить по следующей формуле:
ν=nt
где n — количество «волн», прошедших мимо наблюдателя.
Тогда скорость волны равна:
v=λν=λnt=1·105=2 (мс)
Уравнение бегущей волны
Колебания гармонической волны в любой точке происходят по гармоническому закону с одной и той же амплитудой. Найдем уравнение, описывающее колебательный процесс в любой точке пространства при распространении гармонической волны.
Будем рассматривать волну, бегущую по длинному тонкому резиновому шнуру. Ось Ox направим вдоль шнура, а начало отсчета свяжем с левым концом шнура. Смещение любой колеблющейся точки шнура от положения равновесия обозначим буквой s. Для описания волнового процесса необходимо знать значение s в любой точке шнура в любой момент времени. Следовательно, нужно знать вид функции:
s = s(x, t)
Заставим конец шнура (точка х = 0) совершать гармонические колебания с частотой ω. Если начальную фазу колебаний считать равной 0, то колебания этой точки будут происходить по закону:
s = smaxsin ωt
smax — амплитуда колебаний (рис. а).
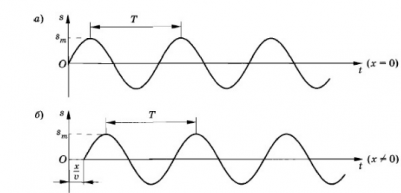
Колебания распространяются вдоль шнура (оси Ox) со скоростью v и в произвольную точку шнура с координатой х придут спустя время, которое можно определить следующим выражением:
τ=xv
Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ (рис. б). Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой smax, но с другой фазой:
Это уравнение называется уравнением бегущей волны, распространяющейся в положительном направлении оси Ox.
Пример №2. Уравнение бегущей волны имеет вид s(x, t)=0,1sin(2πt−xπ2). Найдите частоту волны, скорость её распространения и длину.
Запишем уравнение бегущей волны:
s=smaxsin [ω(t−τ)]=smaxsin [ω(t−xv)]
Сопоставляя эти два уравнения можно определить, что циклическая частота и скорость распространения соответственно равны:
ω=2π (радс)
v=4 (мс)
Циклическую частоту также можно рассчитать по формуле:
ω=2πν
Тогда частота волны равна:
ν=ω2π=2π2π=1 (Гц)
Тогда длина волны равна:
λ=vν=41=4 (м)
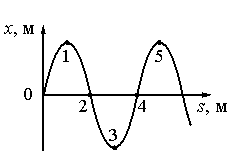 На рисунке показан профиль бегущей волны в некоторый момент времени. Разность фаз колебаний точек 1 и 5 равна
На рисунке показан профиль бегущей волны в некоторый момент времени. Разность фаз колебаний точек 1 и 5 равна