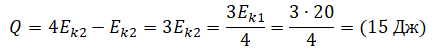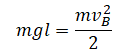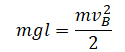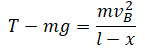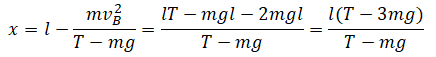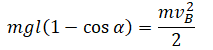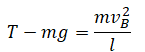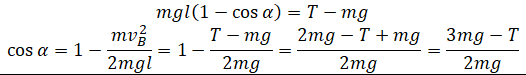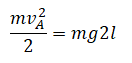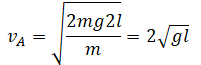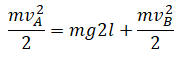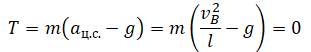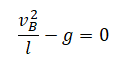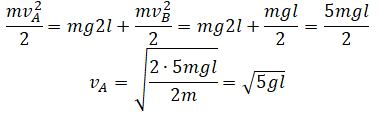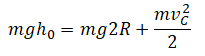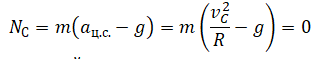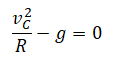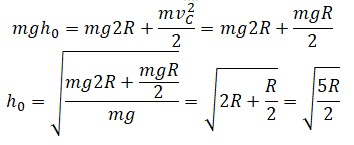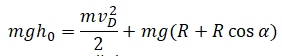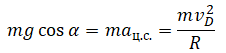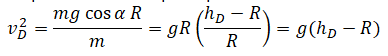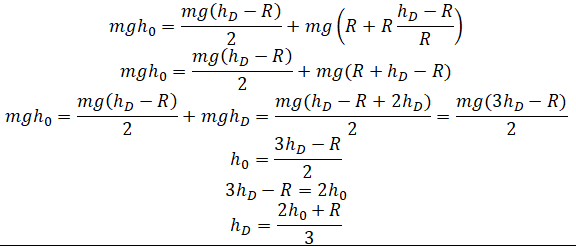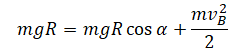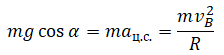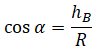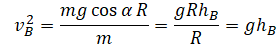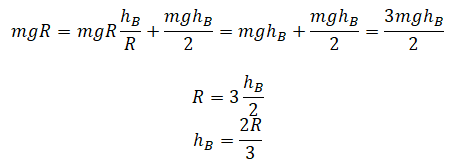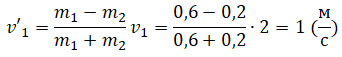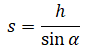Алгоритм решения задач на применение закона сохранения энергии и второго закона Ньютона
Разбор частных случаев закона сохранения энергии
| Задача | Чертеж с решением |
| Легкий стержень прикреплен одним концом к потолку и может совершать колебания в вертикальной плоскости. На другом конце стержня укреплен небольшой груз массы m. Стержень отклонили в горизонтальное положение и отпустили. С какой силой F будет действовать груз на стержень в низшей точке траектории? | 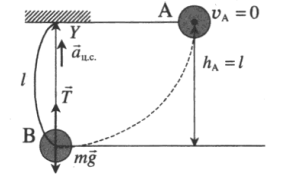
Нулевой уровень — точка В. Закон сохранения энергии:
Второй закон Ньютона в векторной форме для точки В:
Так как центростремительное ускорение равно отношению квадрата скорости к радиусу, а радиус равен длине стержня, проекция на ось ОУ:
Согласно третьему закону Ньютона, F = T. Так как начальная скорость (в точке А) равна нулю, квадрат скорости в точке В можно выразить из формулы перемещения:
Отсюда сила равна:
|
| Нить длиной l с привязанным к ней шариком отклонили на 90о от вертикали и отпустили. На каком наименьшем расстоянии x под точкой подвеса нужно вбить гвоздь, чтобы, налетев на него, нить порвалась? В состоянии покоя нить выдерживает восьмикратный вес шарика. | 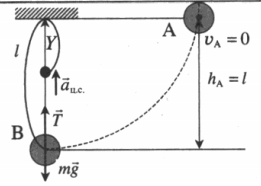
Нулевой уровень — точка В. Закон сохранения энергии:
Вбитый под точкой подвеса гвоздь изменяет радиус движения тела: R = l – x. Второй закон Ньютона в векторной форме для точки В:
Проекция на ОУ:
Отсюда:
Нить выдерживает восьмикратный вес шарика (8mg). Следовательно:
|
| Тяжелый шарик подвешен на нити. Нить может выдерживать максимальное натяжение T. На какой минимальный угол α от положения равновесия нужно отклонить нить с шариком, чтобы он оборвал нить, проходя через положение равновесия? | 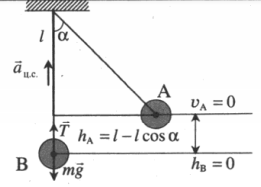
Нулевой уровень — в точке В. Закон сохранения энергии:
Второй закон Ньютона в векторной форме для положения равновесия:
Проекция на ОУ:
Отсюда:
|
| Какую минимальную горизонтальную скорость надо сообщить шарику, чтобы он сделал полный оборот в вертикальной плоскости, если он висит на жестком невесомом стержне длиной l? | 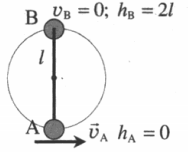
Нулевой уровень — в точке A. Закон сохранения энергии:
Отсюда:
|
| Какую минимальную горизонтальную скорость надо сообщить шарику, чтобы он сделал полный оборот в вертикальной плоскости, если он висит на нити длиной l? | 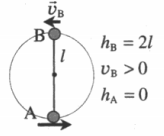
Нулевой уровень — в точке A. Закон сохранения энергии:
Чтобы в верхней точке нить «не упала», шарик должен обладать некоторой скоростью. Минимальную скорость можно рассчитать, приняв, что сила натяжения нити в этом случае равна нулю:
Масса не может быть нулевой, поэтому:
Отсюда:
Вычисляем скорость в начальной точке:
|
| Небольшое тело соскальзывает по наклонной плоскости, плавно переходящей в «мертвую петлю» радиусом R. С какой минимальной высоты должно соскальзывать тело для благополучного прохождения всей петли? Высоту отсчитывают от нижней точки петли. Трением пренебречь. | 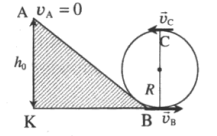
Нулевой уровень — КВ. Закон сохранения энергии:
Чтобы тело успешно прошло «мертвую петлю», оно не должно останавливаться в верхней точке. Минимальная необходимая для продолжения движения скорость определяется для случая, когда сила нормальной реакции опоры равна нулю.
Масса не может быть нулевой, поэтому:
Отсюда:
Вычисляем минимальную высоту в точке А:
|
| Небольшое тело соскальзывает по наклонной плоскости, плавно переходящей в «мертвую петлю» с высоты h0. Радиус петли равен R. На какой высоте оторвется тело от поверхности петли? Высоту отсчитывают от нижней точки петли. Трением пренебречь. | 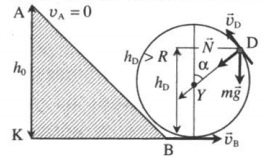
Нулевой уровень — КВ.Закон сохранения энергии:
Второй закон Ньютона в векторной форме:
В точке, в которой тело отрывается от петли, сила нормальной реакции опоры равна 0. Поэтому проекция второго закона Ньютона принимает следующий вид:
Косинус α можно вычислить геометрически:
Отсюда квадрат скорости в точке отрыва равен:
Следовательно:
|
| Небольшое тело соскальзывает без трения с вершины неподвижной полусферы, радиус которой R. На какой высоте тело оторвется от поверхности полусферы? Высоту отсчитывают от основания полусферы. | 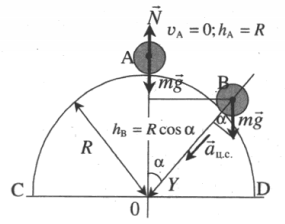
Нулевой уровень — CD. Закон сохранения энергии:
Второй закон Ньютона в векторной форме:
Тело оторвется от петли в точке, в которой сила нормальной реакции опоры будет нулевой. Поэтому проекция второго закона Ньютона на ось ОУ примет вид:
Косинус можно вычислить геометрически:
Отсюда квадрат скорости в точке отрыва равен:
Отсюда:
|
Упругий центральный удар
Если удар центральный, то направления векторов скоростей после взаимодействия лежат на той же прямой, что и до взаимодействия. Поэтому закон сохранения импульса выполняется в проекциях на ось ОХ
Закон сохранения импульса:
m1v1 = m1v’1 + m2v’2
Закон сохранения энергии:
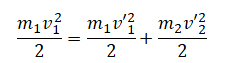
Решив систему уравнений, получаем формулы для расчета проекций скоростей тел на ось ОХ после столкновения:
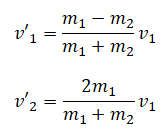
Направление движения налетающего шара после столкновения зависит от массы шаров. Если m1 > m2, то направление сохраняется, и модуль скорости равен:
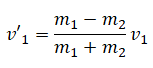
Если m1 < m2, то направление меняется на противоположное, и модуль скорости равен:
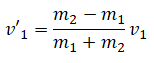
Если m1 = m2, то налетающее тело останавливается. Тогда модуль его силы равен нулю.
Пример №1. Брусок массой 600 г, движущийся со скоростью 2 м/с, сталкивается с неподвижным бруском массой 200 г. Какой будет скорость первого бруска после столкновения? Удар считать центральным и абсолютно упругим.
Переведем единицы измерения в СИ:
600 г = 0,6 кг
200 г = 0,2 кг
Так как масса второго бруска меньше массы первого, скорость первого бруска определяется формулой:
Применение закона сохранения импульса и закона сохранения механической энергии
Если одно тело сталкивается с другим (или пробивает другое), то часть механической энергии переходит во внутреннюю энергию взаимодействующих тел и окружающей среды. Закон сохранения механической энергии «нарушается».
Законом сохранения механической энергии можно пользоваться только до и после столкновений. В момент столкновений следует применять закон сохранения импульса.
Полезные подсказки к задачам!
Снаряд взорвался в точке максимального подъема |
vснар = 0, следовательно pснар = 0 |
| Осколки одинаковой массы | m1 = m2 |
| Массы осколков соотносятся как 1:4 | 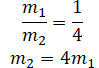 |
| Уравнение координаты при свободном падении | |
| Дальность полета в случае горизонтального броска | 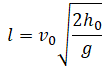 |
| Высота и угол отклонения нити | h = l(1 – cosα) |
Пример №2. Брусок массой 500 г соскальзывает по наклонной плоскости с высоты 0,8 м и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой 300 г. Считая столкновение абсолютно неупругим, определите общую кинетическую энергию брусков после столкновения. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
Переведем единицы измерения в СИ:
500 г = 0,5 кг
300 г = 0,3 кг
Применим закон сохранения импульса:
m1v1 = (m1 + m2)v
Применим закон сохранения энергии:
![]()
Отсюда скорость первого бруска до момента столкновения равна:
![]()
Теперь можем определить скорость двух брусков после столкновения:
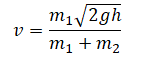
Отсюда кинетическая энергия двух брусков равна:
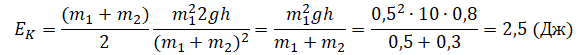
Превращение механической энергии во внутреннюю
Деформации тел при столкновении, влияние сил трения и сопротивления приводят к тому, что механическая энергия преобразуется во внутреннюю. Возможны и обратные превращения. Например, при разрыве снаряда за счет внутренней энергии осколки получают дополнительную механическую энергию.
Полезные подсказки
| Полная механическая энергия в начальный момент времени | E0 = Ek0 + Ep0 |
| Полная механическая энергия в конечный момент времени | E = Ek + Ep |
| Изменение механической энергии | ∆E = E – E0 |
| Механическая энергия переходит во внутреннюю (тепло) |
|∆E| = Q Q — количество теплоты. |
| Увеличение механической энергии в результате взрыва снаряда |
E = E0 +Q Q — добавочная энергия. |
| Изменение механической энергии за счет работы силы трения (силы сопротивления) |
E – E0 = A (Fтр) = –Fтрs Работа силы трения отрицательная, так как угол между вектором перемещения и вектором силы трения равен 180о. Косинус развернутого угла равен –1. |
| Работа силы трения при движении по горизонтали | A (Fтр) = –μmgs |
| Работа силы трения при движении по наклонной плоскости |
A (Fтр) = –μmgs cosα Перемещение равно:
|
| Уравнение скорости при свободном падении | vy = v0y + gyt |
| Дальность полета при броске под углом к горизонту | 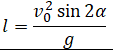 |
Пример №3. Скорость брошенного мяча непосредственно перед ударом о стену была вдвое больше его скорости сразу после удара. Какое количество теплоты выделилось при ударе, если перед ударом кинетическая энергия мяча была равна 20 Дж?
Из условия следует, что v1 = 2v2. К тому же, кинетическая энергия после удара о стену уменьшилась на количество выделенной при ударе теплоты. Поэтому:
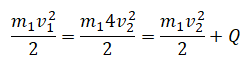
Отсюда:
Ek1 = 4Ek2
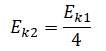
Количество выделенной теплоты равно: