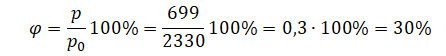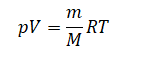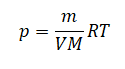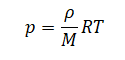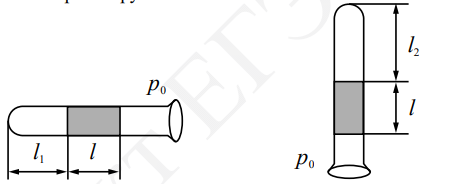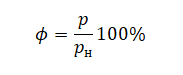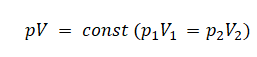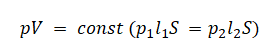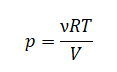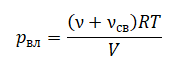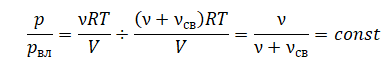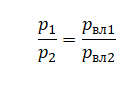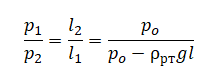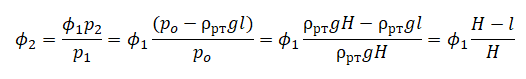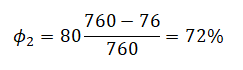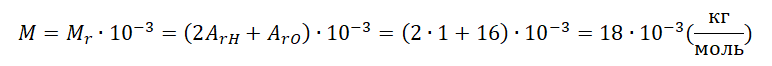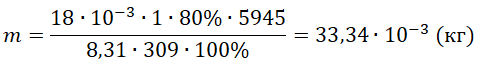Процесс парообразования при испарении происходит только со свободной поверхности жидкости. Испарение бывает при любой температуре, так как всегда найдутся достаточно «быстрые» молекулы, способные преодолеть притяжение молекул жидкости.
Важно! В результате испарения жидкости вылетают самые быстрые молекулы. Поэтому средняя скорость молекул газа уменьшается. Это приводит к уменьшению средней кинетической энергии газа, а следовательно — и температуре.
В открытом сосуде всегда преобладает испарение. В герметично закрытом сосуде устанавливается равновесие между этими процессами.
Динамическое равновесие — это состояние, при котором число испарившихся за единицу времени молекул равно числу сконденсированных. пар, который находится в состоянии динамического равновесия, называется насыщенным.
Давление насыщенного пара в изотермическом процессе не зависит от объема. При уменьшении объема пара «лишние» молекулы воды конденсируются, а при увеличении объема недостаток молекул восполняется за счет испарения. В итоге через некоторое время снова наступает динамическое равновесие.
Пример №1. В сосуде под поршнем при температуре 100 oC находится 2 г водяного пара и такое количество воды. Не изменяя температуры, объем сосуда увеличили в 3 раза. Определить массу воды, перешедшей при этом в пар.
2 г = 10–3 кг
V2 = 3V1
Вода и пар под поршнем находятся в динамическом равновесии. Поэтому при увеличении объема изменение (уменьшение) давления вызывает усиление испарения. Вода кипит при 100 оС только при условии, что давление равно 105 Па. Следовательно, давление насыщенного пара равно именно 105 Па.
Применим уравнение состояния идеального газа для первого и второго случая:
p1V1=m1MRT
p2V2=m2MRT
m1 — масса пара в состоянии 1, m2 — масса газа в состоянии 2.
Внимание! Несмотря на постоянство температуры, применять закон Бойля — Мариотта нельзя, так как в данном случае не сохраняется постоянство массы (количества молекул) пара.
Преобразуем уравнения:
RTM=p1V1m1
RTM=p2V2m2
Приравняем правые части и выразим массу пара в состоянии 2:
p1V1m1=p2V2m2
p1V1m1=p23V1m2
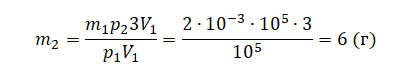
6 г — это масса пара в состоянии 2. Это значит, что в газообразное состояние должно перейти 6 – 2 = 4 г воды. Но под поршнем было лишь 2 г. Следовательно, испарится вся вода.
Влажность воздуха
Выделяют абсолютную и относительную влажности воздуха.
Так как количество испаренных молекул зависит от температуры среды, при одинаковом объеме сосуда и количестве жидкости испарится больше там влаги, где температура выше. Поэтому абсолютная влажность воздуха не дает представления о том, насколько насыщенным является пар. В связи с этим было введено понятие относительной влажности воздуха.
Пример №2. Парциальное давление водяного пара в воздухе при 20 оС равно 699 Па, а давление насыщенных паров при этой температуре равно 2330 Па. Определить относительную влажность воздуха.