Основные законы геометрической оптики были известны задолго до установления физической природы света. Большая часть из них выводятся из общего принципа, описывающего поведение волн. Впервые этот принцип выдвинул современник Ньютона Христиан Гюйгенс.
Чтобы, зная положение волновой поверхности в момент времени t, найти ее положение в следующий момент времени t + ∆t, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени. Этот принцип подходит для описания волн любой природы (световых, механических, электромагнитных и пр.).
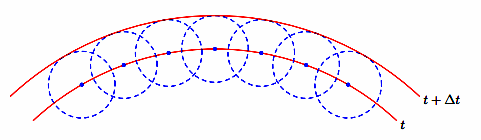
Для механических волн принцип Гюйгенса имеет наглядное толкование: частицы среды, до которых доходят колебания, колеблясь, приводят в движение соседние частицы среды, с которыми они взаимодействуют.
Закон прямолинейного распространения света
Опытным доказательством этого закона служат резкие тени, отбрасываемые непрозрачными телами при освещении светом источника небольших размеров («точечного источника»).

Другим доказательством может служить известный опыт по прохождению света далекого источника сквозь небольшое отверстие, в результате чего образуется узкий световой пучок. Этот опыт приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет.

Пример №1. Здание, освещенное солнечными лучами, отбрасывает тень длиной L = 36 м. Вертикальный шест высотой h = 2,5 м отбрасывает тень длиной l = 3 м. Найдите высоту H здания.
Так как шест и здание расположены вертикально, они параллельны. Так как на них светит один и тот же источник света, то угол падения лучей одинаков. Следовательно, треугольники, образованные стеной зданий, лучом солнца и землей, а также землей, лучом солнца и шестом, подобны. Отсюда можно сделать вывод, что отношение высоты здания к высоте шеста будет отношению длины тени здания к длине тени шеста:
Hh=Ll
H2,5=363=12
H=12·2,5=30 (м)
Закон отражения света
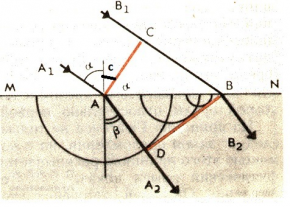
Рассмотрим отражение плоской волны (см. рис. ниже).
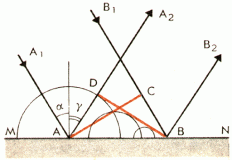
Пусть:
- MN — отражающая поверхность.
- A1A и B1B — два параллельных луча падающей плоской волны.
- AC — волновая поверхность плоской волны.
- α и γ— угол падения и отражения лучей A1A и B1B.
Волновую поверхность отраженной волны можно получить, если провести огибающую вторичных волн, центры которых лежат на границе раздела сред. Различные участки волновой поверхности AC достигают отражающей границы неодновременно. Возбуждение колебаний в точке A начинается раньше, чем в точке B, на время Δt=CBv (v — скорость волны).
В момент, когда волна достигнет точки B, и в этой точке начнется возбуждение колебаний, вторичная волна в точке A уже будет представлять собой полусферу радиусом r = AD = v∆t = CB. Радиусы вторичных волн от источников, находящихся между точками A и B, меняются так, как показано на рисунке выше.
Огибающей вторичных волн является плоскость DB, касательная к сферическим поверхностям. Она является волновой поверхностью отраженной волны. Отраженные лучи AA2 и BB2 перпендикулярны волновой поверхности DB. Между ними образуется угол γ, являющийся углом отражения.
Так как AD = CB и треугольники ADB и ACB прямоугольные, то углы DBA и CAB равны. Но угол α= ∠CAB, а γ= ∠DBA как углы с перпендикулярными сторонами. Следовательно, α=γ.
Пример №2. Луч света падает на плоское зеркало. Угол падения α равен 20°. Чему равен угол между падающим и отражённым лучами?
Поскольку, согласно закон отражения света, угол падения равен углу отражения, то угол между падающим и отражённым лучами равен удвоенному углу α. Следовательно, он равен 40°.
Закон преломления света
На границе двух разнородных сред свет меняет направление распространения. Часть его энергии возвращается в первую среду, то есть, происходит отражение света. Если же вторая среда прозрачна, то часть света проходит через границу, разделяющую первому и вторую среду. При этом он меняет свое направление. Это явление называется преломлением света.
Преломление света на границе двух сред легко продемонстрировать с помощью стакана, воды и карандаша. Если опустить карандаш в пустой стакан, то он будет выглядеть таким же прямым, как и всегда (см. рисунок слева). Если же опустить карандаш в стакан, заполненный водой, мы увидим, что его часть под водой будто бы «преломилась».

Закон преломления света, который определяет взаимное расположение луча падающего, луча преломленного и перпендикуляра, восстановленного в точке падения, был открыт опытным путем в XVII веке. Но его можно доказать, основываясь на принципе Гюйгенса.
Известно, что скорость света достигает максимального значения только в вакууме. При распространении в среде скорость света снижается. Преломление света при переходе из одной среды в другую вызвано различием в скоростях распространения света в той и другой среде. Обозначим скорость распространения волны в первой среде как v1, а во второй — как v2.
Пусть на плоскую границу раздела двух сред (к примеру, из воздуха в воду) падает плоская световая волна (см. рисунок выше). Волновая поверхность AC перпендикулярна лучам A1A и B1B. Поверхности MN сначала достигнет луч A1A. B1B достигнет ее через некоторое время, которое можно определить отношением:
Δt=CBv1
В момент, когда вторичная волна в точке B только начинает возбуждаться, волна от точки A уже имеет вид полусферы, радиус которой определяется выражением:
AD=v2Δt
Волновую поверхность преломленной волны можно получить, проведя поверхность, касательную всем вторичным волнам во второй среде, центры которых лежат на границе раздела сред. В данном случае, ею является плоскость BD. Она является огибающей вторичных волн.
Угол падения α равен CAB в треугольнике ABC (стороны одного из этих углов перпендикулярны сторонам другого). Следовательно:
CB=v1Δt=ABsinα
Угол преломления β равен углу ABD в треугольнике ABD. Поэтому:
AD=v2Δt=ABsinβ
Поделим первое выражение на второе и получим:
sinαsinβ=v1v2=n
Пример №3. Угол падения параллельных лучей на плоскопараллельную пластинку равен 60о. Найдите расстояние между точками, в которых из пластины выходят параллельные лучи, если расстояние между лучами, прошедшими сквозь пластину, равно 0,7 м.
Сначала построим рисунок хода лучей до пластины, внутри нее и после нее. Расстояние между лучами, прошедшими сквозь пластину, обозначим за l. Оно равна длине перпендикуляра, соединяющего эти лучи.
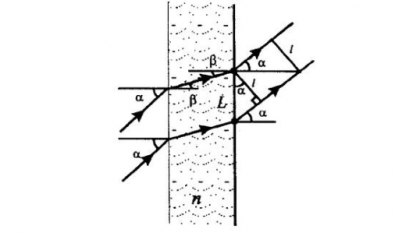
Значение величины угла β, который составляет нормаль к пластине и направлением распространения луча в ней, определяется законом преломления света:
sinαsinβ=n
Луч выходит из пластины под некоторым углом γ таким, что:
sinβsinγ=1n
Следовательно:
n=sinγsinβ=sinαsinβ
Отсюда: sinγ=sinα или γ= α. Если вспомнить геометрические законы, можно сделать вывод, что расстояние между пластинами, являющееся гипотенузой прямоугольного треугольника, можно вычислить путем деления катета на косинус угла между ним и гипотенузой:
L=lcos60°=0,70,5=1,4 (м)
Величина n — относительный показатель преломления.
Физический смысл показателя преломления заключается в том, что он равен отношению скоростей света в средах, на границе между которыми происходит преломление.
n=v1v2
Различают также абсолютный показатель преломления — показатель преломления среды относительно вакуума. Он равен синусу угла падения к синусу угла преломления при переходе светового луча из вакуума в данную среду.
Поскольку в вакууме скорость света максимальна, абсолютный показатель преломления можно выразить формулой:
n=cv1
где v1 — скорость света в среде, c — скорость света в вакууме.
Между абсолютными и относительными показателями преломления есть взаимосвязь. Пусть скорость распространения света в первой среде равна v1, во второй — v2. Тогда абсолютные показатели преломления для первой и второй среды равны:
n1=cv1
n2=cv2
Тогда относительный показатель преломления при переходе света из первой среды во вторую будет равен отношению абсолютного показателя преломления второй среды к абсолютному показателю преломления первой среды:
n=v1v2=n2n1
Пример №4. Определить показатель преломления воды относительно алмаза.
n=nвnа
Абсолютные показатели преломления воды и алмаза — постоянные табличные величины.
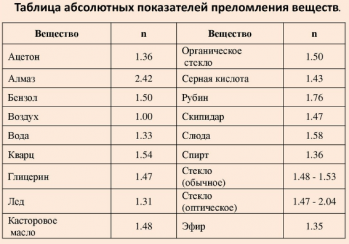
n=1,332,42≈0,55
Полное отражение
Закон преломления света позволяет объяснить интересное и практически важное явление — полное отражение света.
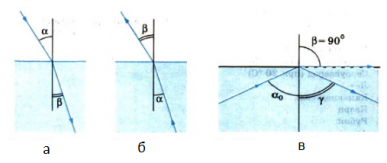
При прохождении света из оптически менее плотной среды в более плотную, к примеру, из воздуха в стекло или воду, v1>v2. Следовательно, согласно закону преломления показатель преломления n > 1. Поэтому α > β (см. рисунок а). В результате преломления луч приближается к перпендикуляру, восстановленному к точке падения луча.
Если же направить луч света в обратном направлении — из оптически более плотной среды в оптически менее плотную вдоль ранее преломленного луча (см. рисунок б), то закон преломления запишется следующим образом:
sinαsinβ=v2v1=1n
Преломленный луч по выходе из оптически более плотной среды будет направлен по линии ранее падавшего луча, поэтому α < β, т. е. преломленный луч в этом случае отдаляется от перпендикуляра, восстановленного в точке падения к границе раздела сред. По мере увеличения угла α угол преломления β также увеличивается. При этом, согласно закону преломления света, он всегда будет больше угла α. Наконец, при некотором угле падения α значение угла преломления β приблизится к 90°, и преломленный луч будет направлен почти по границе раздела двух сред (см. рисунок в). Наибольшему возможному углу преломления β = 90° соответствует угол падения α0.
Попробуем выяснить, что произойдет при α > α0. При падении света на границу двух сред световой луч, как мы уже говорили ранее, частично отражается и частично преломляется. Но при α > α0 преломление света невозможно. Значит, луч должен полностью отразиться. Это явление и называется полным отражением света.
Примеры полного отражения света:
- блеск от ограненного алмаза;
- блеск капель росы на солнце;
- внутреннее отражение предметов, находящихся под водой.

При sin β = 1 (что соответствует углу 90°) угол полного отражения можно определить по формуле:
sinα0=1n
Пример №5. Луч света, идущий из толщи воды, полностью отражается от ее поверхности. Выйдет ли луч в воздух, если на поверхность воды налить слой кедрового масла?
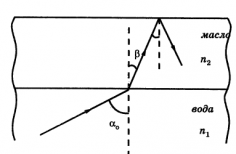
Синус угла полного отражения для луча, идущего из воды к воздуху:
sinα0=1n1
sinα0 n1=1
где n1 — показатель преломления воды.
Запишем закон преломления света для случая, когда на поверхность воды налито масло:
Тогда синус угла полного отражения для луча, идущего из воды к маслу:
sinα0sinβ=n2n1
где n2 — показатель преломления масла.
Тогда:
sinβ=1n2
Эта формула соответствует случаю, когда угол β является углом полного отражения. Следовательно, луч света за пределы масляной пленки в воздух не выйдет.
Практическое применение явления полного отражения света
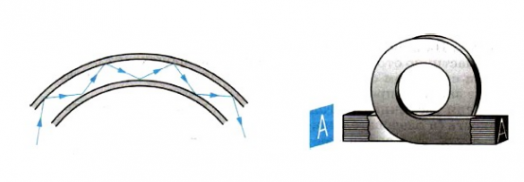
Явление полного отражения света применяют в волоконной оптике для передачи света и изображения по пучкам прозрачных гибких волокон — световодов. Световод — это стеклянное волокно цилиндрической формы, покрытое оболочкой из прозрачного материала с меньшим, чем у волокна, показателем преломления.
За счет многократного полного отражения свет может быть направлен, либо по прямому, либо по изогнутому пути (см. рисунок слева). Волокна собираются в жгуты. При этом по каждому из волокон передается какой-нибудь элемент изображения (см. рисунок справа). Жгуты из волокон используются, например, в медицине для исследования внутренних органов.
В последнее время волоконная оптика широко используется для быстрой передачи компьютерных сигналов. По волоконному кабелю передается модулированное лазерное излучение.
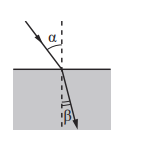 Плоская световая волна переходит из воздуха в глицерин (см. рисунок). Что происходит при этом переходе с периодом электромагнитных колебаний в световой волне и с длиной волны?
Для каждой величины определите соответствующий характер изменения:
Плоская световая волна переходит из воздуха в глицерин (см. рисунок). Что происходит при этом переходе с периодом электромагнитных колебаний в световой волне и с длиной волны?
Для каждой величины определите соответствующий характер изменения:

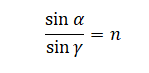
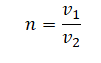
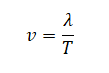


 Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
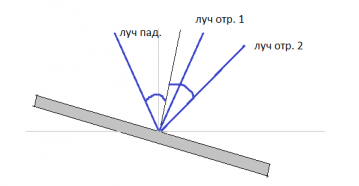
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.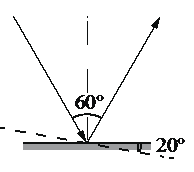 Свет падает на горизонтальное плоское зеркало. Угол между падающим и отражённым лучами равен 60°. Каким станет угол между этими лучами, если повернуть зеркало на 20°, как показано на рисунке?
Свет падает на горизонтальное плоское зеркало. Угол между падающим и отражённым лучами равен 60°. Каким станет угол между этими лучами, если повернуть зеркало на 20°, как показано на рисунке?