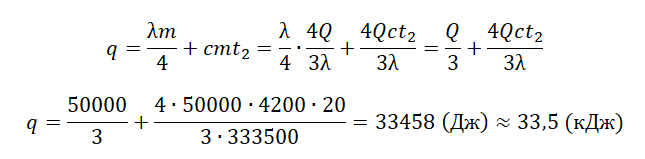Фазовые переходы и уравнение теплового баланса | теория по физике 🧲 термодинамика

Определение

Фазовые переходы — это термодинамические процессы, приводящие к изменению агрегатного состояния вещества.

Плавление и отвердевание

Определение

Плавление — переход вещества из твердого состояния в жидкое.

Для расчета количества теплоты, необходимого для процесса плавления, следует применять формулу:

$Q = λ m$

m — масса вещества, λ (Дж/кг) — удельная теплота плавления.

Плавление каждого вещества происходит при определенной температуре, которую называют температурой плавления. Все проводимое тепло идет на разрушение кристаллической решетки, при этом увеличивается потенциальная энергия молекул. Кинетическая энергия остается без изменения и температура в процессе плавления не изменяется.

Удельная теплота плавления показывает, какое количество теплоты необходимо сообщить 1 кг данного вещества, чтобы перевести его из твердого состояния в жидкое при условии, что оно уже нагрето до температуры плавления. В процессе отвердевания 1 кг данной жидкости, охлажденной до температуры отвердевания, выделится такое же количество теплоты.

Внимание! Удельная теплота плавления — табличная величина.

Определение

Отвердевание, или кристаллизация — переход состояния из жидкого состояния в твердое (это процесс, обратный плавлению).

Отвердевание происходит при той же температуре, что и плавление. В процессе отвердевания температура также не изменяется. Количество теплоты, выделяемое в процессе отвердевания:

$Q = - λ m$

Парообразование и конденсация

Определение

Парообразование, или кипение — переход вещества из жидкого состояния в газообразное.

Количество теплоты, необходимое для процесса кипения, вычисляют по формуле:

$Q = r m$

m — масса вещества, r (Дж/кг) — удельная теплота парообразования.

Парообразование происходит при определенной температуре, которую называют температурой кипения. В отличие от испарения, процесс парообразования идет со всего объема жидкости. Несмотря на то, что к кипящему веществу подводят тепло, температура не изменяется. Все затраты энергии идут на увеличение промежутком между молекулами. Температура кипения зависит от рода вещества и внешнего атмосферного давления.

Удельная теплота парообразования показывает, какое количество теплоты необходимо затратить, чтобы перевести в пар 1 кг жидкости, нагретой до температуры кипения. Такое же количество теплоты выделится в процессе конденсации 1 кг пара, охлажденного до температуры конденсации.

Внимание! Удельная теплота парообразования — табличная величина.

Определение

Конденсация — процесс, обратный кипению. Это переход вещества из газообразного состояния в жидкое.

Конденсация происходит при температуре кипения, которая также не изменяется во время всего процесса. Количество теплоты, выделяемое в процессе конденсации:

$Q = - r m$

Тепловые процессы при нагревании и охлаждении

Все фазовые переходы, а также процессы нагревания и остывания вещества можно отобразить графически. Посмотрите на график фазовых переходов вещества:

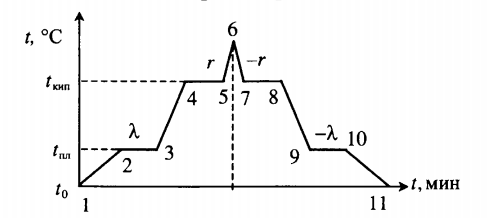
Он показывает зависимость температуры вещества от времени в процессе его нагревания и остывания. Опишем процессы, отображаемые на графике, в таблице.

Процесс	Что происходит	Количество выделенной теплоты
1–2	Нагревание твердого тела	$Q = c_{т} m (t_{п л} - t_{0})$ с_т — удельная теплоемкость вещества в твердом состоянии.
2–3	Плавление при температуре плавления (t_пл)	$Q = λ m$
3–4	Нагревание жидкости	$Q = c_{ж} m (t_{к и п} - t_{п л})$ с_ж — удельная теплоемкость вещества в жидком состоянии.
4–5	Кипение при температуре кипения (t_кип)	$Q = r m$
5–6	Нагревание пара	$Q = c_{п} m (t - t_{к и п})$ с_п — удельная теплоемкость вещества в газообразном состоянии.
6–7	Охлаждение пара	$Q = c_{п} m (t_{к и п} - t)$
7–8	Кипение при температуре кипения (t_кип)	$Q = - r m$
8–9	Охлаждение жидкости	$Q = c_{ж} m (t_{п д} - t_{к и п})$
9–10	Отвердевание при температуре плавления (t_пл)	$Q = - λ m$
10–11	Охлаждение твердого тела	$Q = c_{т} m (t_{0} - t_{п л})$

Внимание! На участках 2–3 и 9–10 вещество частично находится в жидком и твердом состояниях, а на 4–5 и 7–8 — в жидком и газообразном.

Частные случаи тепловых процессов

Что происходит	График	Формула количества теплоты
Полностью растопили лед, имеющий отрицательную температуру.		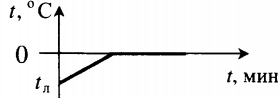$Q = c_{л} m (t_{п л} - t_{л}) + λ m$ c_л — удельная теплоемкость льда, tл — начальная температура льда.
Лед, взятый при отрицательной температуре, превратили в воду при комнатной температуре.		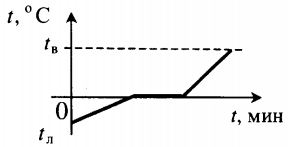$Q = c_{л} m (t_{п л} - t_{л}) + λ m + c_{в} m (t_{в} - t_{п л})$ c_в — удельная теплоемкость воды.
Взяли лед при температуре 0 ^оС и полностью испарили.		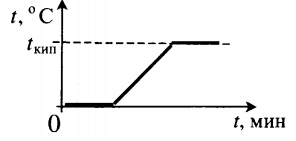$Q = λ m + c_{в} m (t_{к и п} - t_{п л}) + r m$
Взяли воду при комнатной температуре и половину превратили в пар.		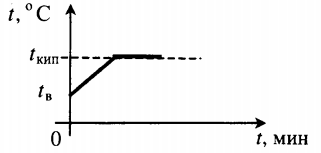$Q = c_{в} m (t_{к и п} - t_{в}) + r \frac{m}{2}$

Подсказки к задачам

Единицы измерения

Температуру можно оставлять в градусах Цельсия, так как изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах.

Кипяток

Вода, которая при нормальном атмосферном давлении имеет температуру в 100 ^оС.

Объем воды 5 л

m = 5 кг, так как:

$m = ρ V =103\cdot 5 \cdot 10^{- 3} м^{3} = 5 к г$

Внимание! Равенство V (л) = m (кг) справедливо только для воды.

Пример №1. Какое количество теплоты нужно сообщить льду массой 2 кг, находящемуся при температуре –10 ^оС, чтобы превратить его в воду и нагреть ее до температуры +30 ^оС?

Можно выделить три тепловых процесса:

Нагревание льда до температуры плавления.
Плавление льда.
Нагревание воды до указанной температуры.

Поэтому количество теплоты будет равно сумме количеств теплоты для каждого из этих процессов:

${Q = Q}_{1} + Q_{2} + Q_{3}$

$Q = c_{л} m (0 - t_{1}) + λ m + c_{в} m (t_{2} - 0)$

Удельные теплоемкости и удельную теплоту плавления смотрим в таблицах:

Удельная теплоемкость льда = 2050 Дж/(кг∙К).
Удельная теплоемкость воды = 4200 Дж/(кг∙К).
Удельная теплота плавления льда = 333,5∙10³ Дж/кг.

Отсюда:

$Q = 2050 \cdot 2 (0 - (- 10)) + 333, 5 \cdot 10^{3} \cdot 2 + 4220 \cdot 2 \cdot 30 = 961200 (д ж) = 961, 2 (к Д ж)$

Уравнение теплового баланса

Суммарное количество теплоты, которое выделяется в теплоизолированной системе равно количеству теплоты (суммарному), которое в этой системе поглощается.

Математически уравнение теплового баланса с учетом знаков количества теплоты записывается так:

$Q_{о т д} = {- Q}_{п о л}$

Отданное количество теплоты меньше нуля (Q_отд < 0), а полученное количество теплоты положительно (Q_получ > 0).

Подсказки к задачам на уравнение теплового баланса

Теплообмен происходит в калориметре	Потерями энергии можно пренебречь.
Жидкость нагревают в некотором сосуде	Начальные и конечные температуры жидкости и сосуда совпадают.
В жидкость опускают термометр	Через некоторое время он покажет конечную температуру жидкости и термометра.
Мокрый снег	Содержит воду и лед при 0 ^оС. Учтите, что лед плавится, если он находится при температуре 0 ^оС и получает энергию от более нагретого тела. Вода кристаллизируется при температуре 0 ^оС, если она отдает энергию более холодному телу. Если лед и вода находятся при температуре 0 ^оС, то никаких агрегатных переходов между ними не происходит.

Частные случаи теплообмена

В воду комнатной температуры бросили ком снега, содержащий некоторое количество воды, после чего установилась некоторая положительная температура.	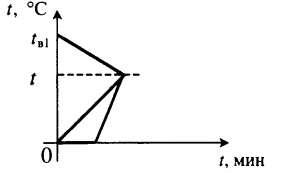Уравнение теплового баланса: $Q_{1} + Q_{2} + Q_{3} = 0$ $c_{в} m_{в 1} (t - t_{в 1}) + c_{в} m_{в 2} (t - 0) + λ m_{л} + c_{в} m_{л} (t - 0) = 0$
Для получения некоторой положительной температуры воды используют горячую воду и лед, имеющий отрицательную температуру.	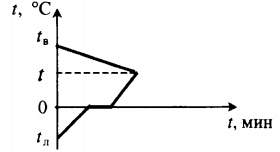Уравнение теплового баланса: $Q_{1} + Q_{2} = 0$ $c_{в} m_{в} (t - t_{в}) + c_{л} m_{л} (0 - t_{л}) + λ m_{л} + c_{в} m_{л} (t - 0) = 0$
В воду комнатной температуры бросают раскаленное твердое тело, в результате часть воды испаряется.	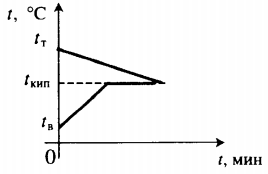Уравнение теплового баланса: $Q_{1} + Q_{2} = 0$ $c_{т} m_{т} (100 - t_{т}) + c_{в} m_{в} (100 - t_{в}) + r m_{п} = 0$
Воду комнатной температуры нагревают до кипения, вводя пар при t = 100 ^оС.	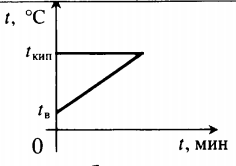Уравнение теплового баланса: $Q_{1} + Q_{2} = 0$ $- r m_{п} + c_{в} m_{в} (100 - t_{в}) = 0$
Лед, имеющий температуру плавления, нагревают до положительной температуры, вводя пар при t = 100 ^оС.	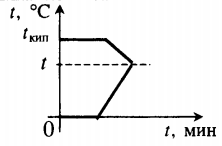Уравнение теплового баланса: $Q_{1} + Q_{2} = 0$ $- r m_{п} + c_{в} m_{п} (t - t_{к и п}) + λ m_{л} + c_{в} m_{л} (t - t_{п л}) = 0$

Пример №2. В кастрюлю, где находится вода объемом 2 л при температуре 25 ^оС, долили 3 л кипятка. Какая температура воды установилась?

2 л = 2 кг

3 л = 3 кг

Количество теплоты, отданное кипятком, равно количеству теплоты, принятому более прохладной водой. Поэтому:

$c m_{1} (t - t_{0}) = - c m_{2} (t - t_{к и п})$

Или:

$m_{1} (t - t_{0}) = - m_{2} (t - t_{к и п})$

$m_{1} t + m_{2} t = m_{1} t_{0} + m_{2} t_{к и п}$

${(m}_{1} + m_{2}) t = m_{1} t_{0} + m_{2} t_{к и п}$

$t = \frac{m_{1} t_{0} + m_{2} t_{к и п}}{m_{1} + m_{2}}$

$t = \frac{2 \cdot 25 + 3 \cdot 100}{2 + 3} = \frac{350}{5} = 70 (° C)$

Взаимные превращения механической и внутренней энергии

Если в тексте задачи указан процент одного вида энергии, перешедший в другой, то он указывается в виде десятичной дроби перед этой энергией, которой тело обладало вначале.

Частные случаи закона сохранения энергии

При неупругом ударе о стенку пуля нагрелась	$\frac{m v^{2}}{2} = c m Δ t$
Тело падает с некоторой высоты и в момент падения нагревается	$m g h = c m Δ t$
В результате того, что пуля пробивает стену, ее скорость уменьшается, 50% выделившейся при этом энергии идет на нагревание пули	$0, 5 (\frac{m v_{0}^{2}}{2} - \frac{m v^{2}}{2}) = c m Δ t$
Летящая пуля при ударе о стенку расплавилась. Начальная температура пули меньше температуры плавления	$\frac{m v^{2}}{2} = c m Δ t + λ m$
Капля воды, падая с некоторой высоты, в момент удара испарилась. Температура капли у поверхности земли меньше температуры кипения. На нагрев пошло 60% выделившейся механической энергии	$0, 6 m g h = c m Δ t + r m$
Вследствие сгорания топлива ракета поднялась на некоторую высоту	$q m_{т о п} = m_{р} g h$
Вследствие сгорания топлива снаряд приобрел некоторую скорость, и на это было затрачено 25% энергии	$0, 25 q m_{т о п} \frac{m_{с} v^{2}}{2}$

Пример №3. Свинцовая дробинка, летящая со скоростью 100 м/с, попадает в доску и входит в нее. 52% кинетической энергии дробинки идет на ее нагревание. На сколько градусов нагрелась дробинка? Удельная теплоемкость свинца 130 Дж/(кг∙К).

Запишем закон сохранения энергии для этого случая:

$0, 52 \frac{m v^{2}}{2} = c m Δ t$

$Δ t = \frac{{0, 52 v}^{2}}{2 c} = \frac{0, 52 \cdot 100^{2}}{2 \cdot 130} = 20 (К)$

Примеры КПД

Устройство	Полезная энергия (работа), затраченная энергия (полная работа)	КПД
Электронагреватель, электроплитка, электрочайник, кипятильник.	$Q_{п о л е з н} = c m Δ T$ Иногда: $Q_{п о л е з н} = c m Δ T + r m$ $W_{з а т р} = P t$ $(п р о и з в е д е н и е м о щ н о с т и н а в р е м я)$	$η = \frac{c m Δ T}{P t} 100 %$
Газовая горелка, паровая турбина, спиртовка, плавильная печь.	$Q_{п о л е з н} = c m Δ T$ $Q_{з а т р} = q m_{т о п}$	$η = \frac{c m Δ T}{q m_{т о п}} 100 %$
Двигатель автомобиля, самолета.	$A_{п о л е з н} = N t = N \frac{s}{v}$ $Q_{з а т р} = q m_{т о п}$	$η = \frac{c m Δ T}{v q m_{т о п}} 100$
Ружье с пороховым зарядом, пушка	$E_{п о л е з н} = \frac{m v^{2}}{2}$ $Q_{з а т р} = q m_{п о р}$	$η = \frac{m v^{2}}{2 q m_{п о р}} 100$

Внимание! Если в задаче указано время, в течение которого происходит один тепловой процесс, а спрашивают о времени протекания другого, то считайте, что мощность нагревателя или холодильника постоянна:

$\frac{Q_{1}}{t_{1}} = \frac{Q_{2}}{t_{2}}$

Пример №4. Для нагревания на электроплитке некоторого количества воды от 20 до 100 ^оС потребовалась 21 минута. Сколько времени после этого необходимо для полного испарения воды? Удельная теплоемкость воды 4200 Дж (кг∙К), удельная теплота парообразования 2,24 МДж/кг.

Будем считать, что мощность электроплитки постоянна. Поэтому:

$\frac{Q_{1}}{t_{1}} = \frac{Q_{2}}{t_{2}}$

Количество теплоты, сообщенное воде при нагревании:

$Q_{1} = с m (t_{2} - t_{1})$

Количество теплоты, которое нужно сообщить, чтобы вода полностью испарилась:

$Q_{1} = r m$

Отсюда:

$\frac{с m (t_{2} - t_{1})}{t_{1}} = \frac{r m}{t_{2}}$

Текст: Алиса Никитина, 20.1k 👀

Задание ЕГЭ-Ф-ДВ2023-8

Температура куска металла с удельной теплоёмкостью 900 Дж/(кг∙К) понизилась со 120 °С до 40 °С. При этом выделилось количество теплоты, равное 108 кДж. Чему равна масса этого куска металла? Ответ дайте в кг.

Алгоритм решения:

Записать исходные данные.
Перевести единицы измерения величин в СИ.
Записать формулу количества теплоты для описанного в задаче процесса.
Выразить искомую величину (массу вещества).
Подставить известные величины и сделать вычисления.

Решение:

Запишем исходные данные:

Удельная теплоемкость куска металла: c = 900 Дж/(кг∙К).
Начальная температура куска металла: t₁ = 120 ^оС.
Конечная температура куска металла: t₂ = 40 ^оС.
Выделенное количество теплоты: Q = 108 кДж.

Так как нас будет интересовать только изменение температуры, переводить градусы Цельсия в Кельвины нет необходимости. Но выделенное количество теплоты необходимо преобразовать в Джоули:

Q = 108 кДж = 108∙10³ Дж

В описанном процессе кусок металла находится в твердом состоянии и не испытывает фазовых переходов. Он лишь остывает, высвобождая некоторое количество теплоты. Следовательно, количество теплоты определяется формулой:

Тогда:

Отсюда масса равна:

Подставляем известные данные и делаем вычисления:

Ответ: 1,5

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17544

Кусок льда, имеющий температуру 0°С, помещён в калориметр с электронагревателем. Чтобы превратить этот лёд в воду с температурой 12°С, требуется количество теплоты 80 кДж. Какая температура установится внутри калориметра, если лёд получит от нагревателя количество теплоты 60 кДж? Теплоёмкостью калориметра и теплообменом с внешней средой пренебречь.

Ответ:

а) 0°С

б) 4°С

в) 6°С

г) 9°С

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Записать уравнение теплового баланса для первого случая.

3.Вычислить массу льда.

4.Выполнить решение.

Решение

Запишем исходные данные:

• Начальная температура льда: t₀ = 0 ^oC.

• Конечная температура воды в первом случае: t₁ = 12 ^oC.

• Количество теплоты, выделенное электронагревателем в первом случае: Q₁ = 80 кДж.

• Количество теплоты, выделенное электронагревателем во втором случае: Q₂ = 60 кДж.

Составим уравнение теплового баланса для первого случая:

$Q_{1} = λ m + c m t_{1}$

Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.

Найдем массу льда из уравнения теплового баланса для первого случая. Учтем что:

• Удельная теплоемкость воды: c = 4200 Дж/(кг∙К).

• Удельная теплота плавления льда: λ = 333,5 кДж/(кг∙К).

Отсюда:

Чтобы расплавить кусок льда массой 0,5 кг, нужно затратить следующее количество теплоты:

Лед не расплавится весь, так как ему будет сообщено лишь 60 кДж теплоты. Поэтому в калориметре температура будет равна 0 ^оС.

.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18791

Внимательно прочитайте текст задания и выберите верный ответ из списка

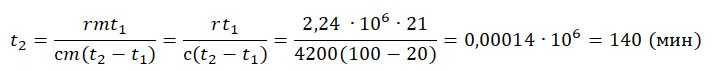
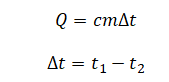
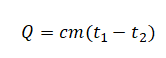
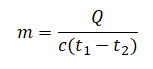
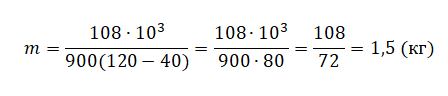
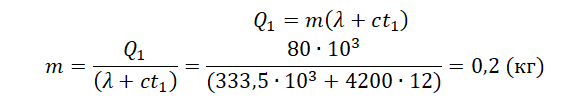
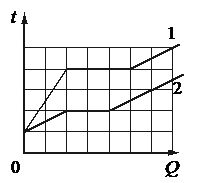На рисунке представлены графики зависимости температуры t двух тел одинаковой массы от сообщённого им количества теплоты Q. Первоначально тела находились в твёрдом агрегатном состоянии.

Используя данные графиков, выберите из предложенного перечня два верных утверждения и укажите их номера. Ответ: а) Температура плавления первого тела в 1,5 раза больше, чем второго. б) Тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии. в) Удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого. г) Оба тела имеют одинаковую удельную теплоту плавления. д) Тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.

Алгоритм решения

Проанализировать каждое из утверждений.
Проверить истинность утверждений с помощью графика.
Выбрать и записать верные утверждения.

Решение

Проверим первое утверждение, согласно которому, температура плавления первого тела в 1,5 раза больше, чем второго.

Если это было бы так, то количество клеток до горизонтального участка графика 1 относилось к количеству клеток до горизонтального участка графика 2 как 3 к 2. Но мы видим, что до 1 графика 4 клетки, до 1 — 2. Следовательно, температура плавления первого тела в 2 раза больше, чем второго.

Первое утверждение неверно.

Проверим второе утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.

Если бы это было так, то соответствующие участки графиков совпадали бы. Только в таком случае температура тел увеличивалась на одну и ту же температуру при получении одного и того же количества теплоты. Но мы видим, что это не так.

Второе утверждение неверно.

Проверим третье утверждение, согласно которому удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого.

Если это было бы так, то первое тело при сообщении телам одинакового количества теплоты нагревалось бы втрое быстрее второго. И это действительно так, потому что температура второго во время нагревания в твердом состоянии увеличилась только на 1 клетку, в то время как температура первого тела — на 2 клетки.

Третье утверждение верно.

Проверим четвертое утверждение, согласно которому оба тела имеют одинаковую удельную теплоту плавления.

Если это было бы так, то протяженность горизонтальных участков обоих графиков была бы одинаковой. Но это не так. Протяженность этого участка для тела 1 составляет 3 клетки, для тела 2 — 2 клетки.

Четвертое утверждение верно.

Проверим пятое утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.

Если бы это было так, то соответствующие участки графиков были параллельными. Только при таком условии при повышении температуры на одно и то же количество градусов тела бы получли одинаковое количество теплоты. И это действительно так.

Пятое утверждение верно.

Вывод: верным утверждения «в» и «д».

Ответ: вд

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22685

В сосуде лежит кусок льда. Температура льда $t_{1} = 0$ °C. Если сообщить ему количество теплоты $Q = 50$ кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры $t_{2} = 20$ °C? Тепловыми потерями на нагрев сосуда пренебречь.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Записать уравнение теплового баланса.

3.Выполнить решение в общем виде.

4.Определить и вычислить искомую величину.

Решение

Запишем исходные данные:

• Начальная температура льда: t₁ = 0 ^oC.

• Конечная температура воды: t₂ = 20 ^oC.

• Количество теплоты, переданное льду изначально: Q = 50 кДж.

• Удельная теплоемкость воды: c = 4200 Дж/(кг∙К).

• Удельная теплота плавления льда: λ = 333,5 кДж/(кг∙К).

50 кДж = 50000 Дж

333,5 кДж = 333500 Дж

Составим уравнение теплового баланса:

$Q_{о б щ} = Q + q$

где q — количество теплоты, необходимое для того, чтобы окончательно растопить лед и нагреть воду:

$q = Q_{2} + Q_{3}$

Мы знаем, что изначально было растоплено 3/4 льда. Поэтому:

$Q = \frac{3 λ m}{4}$

Отсюда масса льда равна:

$m = \frac{4 Q}{3 λ}$

На растопку оставшегося льда уйдет следующее количество теплоты:

$Q_{2} = \frac{λ m}{4}$

На нагревание воды уйдет следующее количество теплоты:

$Q_{3} = c m t_{2}$

Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.

Отсюда:

pазбирался: Алиса Никитина | обсудить разбор

ЕГЭ по физике

Вся теория

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

Плавление и отвердевание

Парообразование и конденсация

Тепловые процессы при нагревании и охлаждении

Частные случаи тепловых процессов

Уравнение теплового баланса

Взаимные превращения механической и внутренней энергии

Примеры КПД

Задание ЕГЭ-Ф-ДВ2023-8

Задание EF17544

Задание EF18791

Задание EF22685

ЕГЭ по физике

Вся теория

Добавить комментарий Отменить ответ