Рассмотрим произвольный участок цепи. Это может быть однородный проводник, к примеру, обмотка электродвигателя или нить лампы накаливания. Пусть за время ∆t через поперечное сечение проводника проходит заряд ∆q. Тогда электрическое поле совершит работу:
A=ΔqU
Но сила тока равна:
I=ΔqΔt
Выразим заряд:
Δq=IΔt
Тогда работа тока равна:
A=IUΔt
Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого совершалась работа.
Выражая через закон Ома силу тока и напряжение, получим следующие формулы для вычисления работы тока:
A=I2RΔt=U2RΔt
Работа тока измеряется в Джоулях (Дж).
Пример №1. Определите работу тока, совершенную за 10 секунд на участке цепи напряжением 200В и силой тока 16 А.
A=IUΔt=16·220·10=35200 (Дж)=35,2 (кДж)
Закон Джоуля-Ленца
В случае, когда на участке цепи не совершается механическая работа, и ток не производит химических действий, происходит только нагревание проводника. Нагретый проводник отдает теплоту окружающим телам.
Закон, определяющий количество теплоты, которое выделяет проводник с током в окружающую среду, был впервые установлен экспериментально английским ученым Д. Джоулем (1818—1889) и русским Э.Х. Ленцем (1804—1865). Закон Джоуля—Ленца сформулирован следующим образом:
Пример №2. Определить, какое количество теплоты было выделено за 2 минуты проводником при напряжении 12 В и сопротивлении 2 Ом.
Используем закон Ома и закон Джоуля—Ленца:
Q=I2RΔt=(UR)2Δt=U2RΔt=1222=72 (Дж)
Мощность тока
Любой электрический прибор (лампа, электродвигатель и пр.) рассчитан на потребление определенной энергии в единицу времени. Поэтому наряду с работой тока очень важное значение имеет понятие мощности тока.
Это выражение для мощности можно переписать в нескольких эквивалентных формах, если использовать закон Ома для участка цепи:
P=IU=I2R=U2R
Пример №3. При силе тока в электрической цепи 0,3 А сопротивление лампы равно 10 Ом. Определите мощность электрического тока, выделяющуюся на нити лампы.
P=I2R=0,32·10=0,9 (Вт)
Выразив силу тока через заряд, прошедший за единицу времени, получим:
P=qUt
Мощность тока равна мощности на внешней цепи. Ее также называют мощностью на нагрузке, полезной мощностью или тепловой мощностью. Ее можно выразить через ЭДС:
P=(εR+r)2R
Мощность тока на внешней цепи будет максимальная, если сопротивление внешней цепи равно внутреннему сопротивлению: R = r.
Pmax=(εr+r)2r=ε24r
Мощность тока внутренней цепи:
Pвнутр=I2r=(εR+r)2r
Полная мощность:
Pполн=I2(R+r)=ε2R+r
Пример №4. ЭДС постоянного тока ε = 2 В, а его внутреннее сопротивление r = 1 Ом. Мощность тока в резисторе, подключенном к источнику, P0 = 0,75 Вт. Чему равно минимальное значение силы тока в цепи?
Используем формулу для нахождения полезной мощности:
P=(εR+r)2R
Применим закон Ома для полной цепи:
I=εR+r
Выразим сопротивление внешней цепи:
R=εI−r
Отсюда:
P=(εεI−r+r)2(εI−r)=I2(εI−r)=Iε−rI2
Так как внутреннее сопротивление равно единице, получаем квадратное уравнение следующего вида:
rI2−Iε+P=0
I2−1I+0,75=0
Решив это уравнение, получим два корня: I = 0,5 и I = 1,5 А. Следовательно, наименьшая сила тока равна 0,5 А.
Подсказки к задачам
| Объем проводника цилиндрической формы |
V=Sl |
| Масса проводника цилиндрической формы |
m=ρV=ρSl |
| Количество теплоты и изменение температуры |
Q=cmΔT |
Конденсатор в цепи постоянного тока
Постоянный ток через конденсатор не идет, но заряд на нем накапливается, и напряжение между обкладками поддерживается. Напряжение на конденсаторе такое же, как на параллельном ему участке цепи.
Ток не проходит через те резисторы, что соединены с конденсатором последовательно. При расчете электрической цепи их сопротивления не учитывают.
Подсказки к задачам
| Электроемкость, заряд и напряжение |
C=qU |
| Напряженность и напряжение |
E=Ud |
| Энергия конденсатора |
W=q22C=CU22 |
| Количество теплоты |
Q=ΔW |
Пример №5. К источнику тока с ЭДС ε = 9 В и внутренним сопротивлением r = 1 Ом подключили параллельно соединенные резистор с сопротивлением R = 8 Ом и плоский конденсатор, расстояние между пластинами которого d = 0,002 м. Какова напряженность электрического поля между пластинами конденсатора?
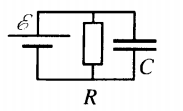
Напряжение на конденсаторе равно напряжению на резисторе, так как он подключен к нему последовательно. Чтобы найти это напряжение, сначала выразим силу тока на этом резисторе:
I=εR+r
Применим закон Ома:
I=UR
Приравняем правые части выражений и получим:
εR+r=UR
Отсюда напряжение на конденсаторе равно:
U=εRR+r
Напряженность электрического поля равна:
E=Ud=εRd(R+r)=9·80,002(8+1)=720,018=4000 (Вм)
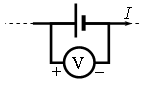 Вольтметр подключён к клеммам источника тока с ЭДС ε = 3 В и внутренним сопротивлением r = 1 Ом, через который течёт ток I = 2 А (см. рисунок). Вольтметр показывает 5 В. Какое количество теплоты выделяется внутри источника за 1 с?
Вольтметр подключён к клеммам источника тока с ЭДС ε = 3 В и внутренним сопротивлением r = 1 Ом, через который течёт ток I = 2 А (см. рисунок). Вольтметр показывает 5 В. Какое количество теплоты выделяется внутри источника за 1 с?
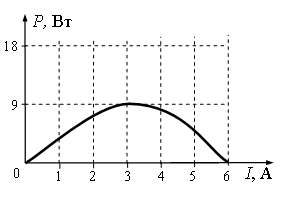 Ученик исследовал зависимость тепловой мощности Р, выделяющейся на реостате R, от силы тока в цепи. При проведении опыта реостат был подключён к источнику постоянного тока. График полученной зависимости приведён на рисунке.
Ученик исследовал зависимость тепловой мощности Р, выделяющейся на реостате R, от силы тока в цепи. При проведении опыта реостат был подключён к источнику постоянного тока. График полученной зависимости приведён на рисунке.