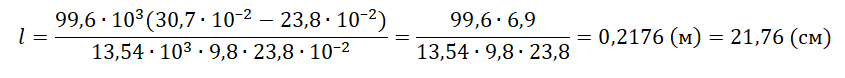Объединенный газовый закон был открыт экспериментально. Он также является следствием основного уравнения состояния идеального газа. Согласно ему:
Объединенный газовый закон применительно к изопроцессам
Объединенный газовый закон объединяет три независимых газовых закона: Бойля — Мариотта, Шарля и Гей-Люссака. Газовые законы действуют в частных случаях — изопроцессах.
Изотермический процесс. Закон Бойля — Мариотта.
Изотермический процесс — термодинамический процесс, происходящий в системе при постоянной температуре и массе:
m = const (m1 = m2)
T = const (T1 = T2)
Для изотермического процесса действует закон Бойля — Мариотта:
Изохорный процесс. Закон Шарля.
Изохорный процесс — термодинамический процесс, происходящий в системе при постоянном объеме и массе:
m = const (m1 = m2)
V = const (V1 = V2)
Для изохорного процесса действует закон Шарля:
Изобарный процесс. Закон Гей-Люссака.
Изобарный процесс — термодинамический процесс, происходящий в системе при постоянном давлении и массе:
m = const (m1 = m2)
p = const (p1 = p2)
Пример №1. Идеальный газ изобарно нагревают так, что его температура изменяется на ∆T = 240 К, а давление — в 1,6 раза. Масса газа постоянна. Найдите начальную температуру газа по шкале Кельвина.
Так как газ нагревают, то:
T2 – T1 = 240 (К)
Отсюда:
T2 = 240 + T1 (К)
p1 = p
p2 = 1,6p
Запишем закон Шарля применительно к данному случаю:
pT1=1,6p240+ T1
Сделаем некоторые преобразования и вычислим начальную температуру:
pT1=1,6p240+ T1
240+ T1=1,6T1
0,6T1=240
T1=2400,6=400 (К)
Подсказки к задачам на газовые законы
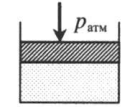 |
Газ под невесомым поршнем: p = pатм p — давление газа; pатм — давление, оказываемое на газ со стороны поршня. |
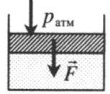 |
На невесомый поршень действует сила: p=pатм+FS F — сила, действующая на поршень; S — площадь поршня. |
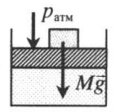 |
На невесомый поршень поставили груз. В данном случае на поршень дополнительно будет действовать сила тяжести: p=pатм+FтяжS=pатм+MgS Fтяж — сила тяжести, действующая на поршень со стороны груза; M — масса груза; g — ускорение свободного падения. |
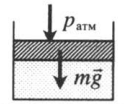 |
Газ под массивным поршнем. В данном случае на него дополнительно будет действовать сила тяжести поршня: p=pатм+mgS m — масса поршня. |
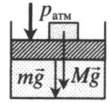 |
На массивный поршень поставили груз. В данном случае на поршень дополнительно будут действовать силы тяжести со стороны поршня и груза: p=pатм+MgS+mgS |
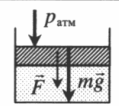 |
На массивный поршень действует сила. В данном случае газ сдавливается как атмосферным давлением, так и силой тяжести поршня, а также силой, которая на него действует: p=pатм+mgS+FS |
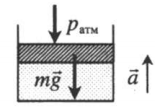 |
Газ, находящийся в цилиндре под массивным поршнем, находится в лифте, ускорение которого направлено вверх. Когда ускорение движения лифта противоположно направлено ускорению свободного падения, вес тел увеличивается. Поэтому: p=pатм+mgS+maS a — модуль ускорения, с которым движется лифт. |
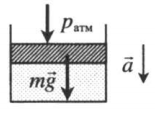 |
Газ, находящийся в цилиндре под массивным поршнем, находится в лифте, ускорение которого направлено вниз. Когда ускорение движения лифта направлено в сторону вектора ускорения свободного падения, вес тел уменьшается. Поэтому: p=pатм+mgS−maS |
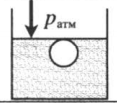 |
«Пузырек у поверхности воды» — на пузырек действует только атмосферное давоение: p = pатм |
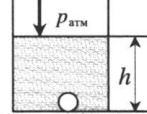 |
«Пузырек на глубине» — на пузырек действует атмосферное давление и давление столба жидкости: p = pатм + ρgh ρ — плотность жидкости; h — глубина, на которой находится пузырек. |
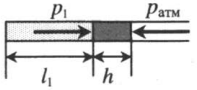 |
Газ, находящийся в горизонтальной пробирке, отделен от атмосферы столбиком ртути. Объем газа можно вычислить, используя параметры пробирки: V1 = l1S V1 — объем газа; l1 — длина части пробирки, которую занимает газ; S — площадь поперечного сечения пробирки. Давление газа равно атмосферному давлению: p1 = pатм |
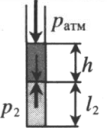 |
Пробирку поворачивают открытым концом вверх. В этом случае кроме атмосферного давления на газ давит давление со стороны ртути: P2 = pатм + ρgh Объем газа можно вычислить, используя параметры пробирки: V2 = l2S |
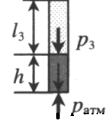 |
Пробирку поворачивают открытым концом вниз. В этом случае сумма давлений газа и ртути в пробирке равна атмосферному давлению. Отсюда давление газа равно: P3 = pатм – ρgh Объем газа можно вычислить, используя параметры пробирки: V3 = l3S |
| Шар или понтон поднимается вверх в воздухе или жидкости | Архимедова сила больше силы тяжести:
FA > Fтяж |
Пример №2. Поршень площадью 10 см2 массой 5 кг может без трения перемещаться в вертикальном цилиндрическом сосуде, обеспечивая при этом герметичность. Сосуд с поршнем, заполненный газом, покоится на полу неподвижного лифта при атмосферном давлении 100 кПа, при этом расстояние от нижнего края поршня до дна сосуда 20 см. Каким станет это расстояние, когда лифт поедет вверх с ускорением, равным 2 м/с2? Изменение температуры газа не учитывать.
10 см2 = 10–3 м2
20 см = 0,2 м
100 кПа = 105 Па
Составим уравнения для 1 и 2 случая. Когда лифт находится в покое, давление газа равно сумме атмосферного давления и давления, оказываемое массивным поршнем:
p1=pатм+mgS
Когда лифт начал двигаться, появилось дополнительное давление, связанное с увеличением веса поршня при ускоренном движении вверх:
p2=pатм+mgS+maS
Так как изменением температуры можно пренебречь, можно считать, что это процесс изотермический. Следовательно:
p1V1 = p2V2
Объемы в 1 и 2 случае будут определяться формулами:
V1 = Sh1
V2 = Sh2
h1 — расстояние от нижнего края поршня до дна сосуда в первом случае. h2 — та же самая величина, но во втором случае (искомая величина).
Запишем закон Бойля — Мариотта для обоих случаев с учетом объемов:
p1V1=Sh1(pатм+mgS)
p2V2=Sh2(pатм+mgS+maS)
Так как это изотермический процесс, правые части уравнений можно приравнять:
Sh1(pатм+mgS)= Sh2(p
атм+mgS+maS)
Отсюда:
Графики изопроцессов
Изопроцессы можно изобразить графически в координатах (p;V), (V;T) и (p;T). Рассмотрим все виды графиком для каждого из процессов.
| Изопроцесс | График в координатах (p;V) | График в координатах (V;T) | График в координатах (p;T) |
| Изотермический (график — изотерма) | 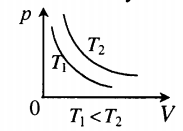
Изотерма в координатах (p;V) — гипербола. Чем ближе изотерма к началу координат и осям, тем меньшей температуре она соответствует. Характер изменения переменных величин хорошо виден на графике. |
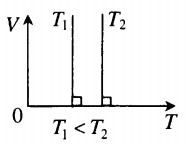
Изотерма в координатах (V;T) — прямая, перпендикулярная оси OT и параллельная оси OV. Чем ближе изотерма к оси OV, тем меньшей температуре она соответствует. С увеличением объема давление уменьшается. |
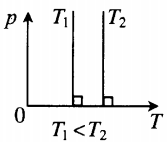
Изотерма в координатах (p;T) — прямая, перпендикулярная оси OT и параллельная оси Op. Чем ближе изотерма к оси Op, тем меньшей температуре она соответствует. С увеличением давления объем уменьшается. |
| Изохорный (график — изохора) | 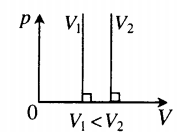
Изохора в координатах (p;V) — прямая, перпендикулярная оси OV и параллельная оси Op. Чем ближе изохора к оси Op, тем меньшему объему она соответствует. С увеличением давления увеличивается температура. |
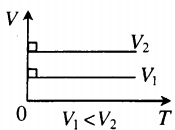
Изохора в координатах (V;T) — прямая, перпендикулярная оси OV и параллельная оси OT. Чем ближе изохора к оси OT, тем меньшему объему она соответствует. С увеличением температуры увеличивается давление. |
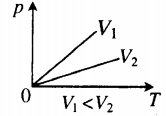
Изохора в координатах (p;T) — прямая, исходящая из начала координат. Чем меньше угол наклона изохоры к оси OT, тем меньшему объему она соответствует. Характер изменения переменных величин хорошо виден на графике. |
| Изобарный (график — изобара) | 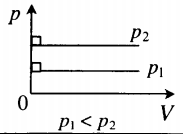
Изобара в координатах (p;V) — прямая, перпендикулярная оси Op и параллельная оси OV. Чем ближе изобара к оси OV, тем меньшему давлению она соответствует. С увеличением объема температура растет. |
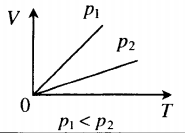
Изобара в координатах (V;T) — прямая, исходящая из начала координат. Чем меньше угол наклона изобары к оси OT, тем меньшему давлению она соответствует. Характер изменения переменных величин хорошо виден на графике. |

Изобара в координатах (p;T) — прямая, перпендикулярная оси Op и параллельная оси OT. Чем ближе изобара к оси OT, тем меньшему давлению она соответствует. С увеличением температуры объем растет. |
Пример №3. На рисунке представлен график циклического процесса. Вычертить его в координатах (p;T).
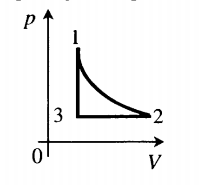
Определим характер изменения величин:
- Процесс 1–2. Гипербола — это изотерма. Следовательно T12 = const. В координатах (p;T) изотерма будет выглядеть как прямая, перпендикулярная оси OT.
- Процесс 2–3. Прямая линия, перпендикулярная оси Op — это изобара. Следовательно p23 = const. В координатах (p;T) изобара будет выглядеть как прямая, перпендикулярная оси Op.
- Процесс 3–1. Прямая линия, перпендикулярная оси OV — это изохора. Следовательно V31 = const. В координатах (p;T) изохора будет выглядеть как прямая, выходящая из начала координат.
Теперь, зная, какими будут графики всех величин в координатах (p;T), можно построить сам график. Он примет следующий вид:
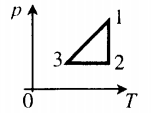
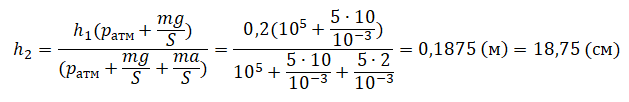

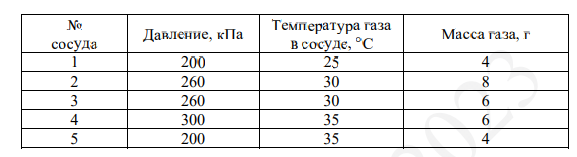 В ответ запишите номера выбранных сосудов.
В ответ запишите номера выбранных сосудов.
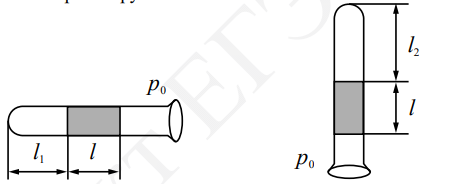

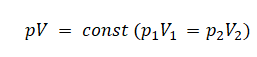
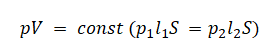
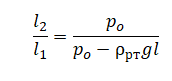
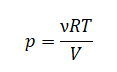
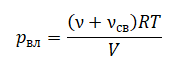
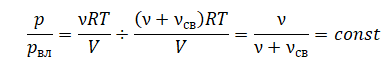
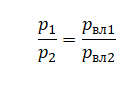
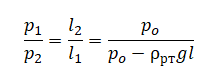
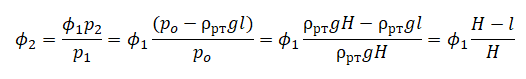
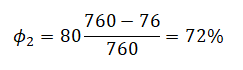
 На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.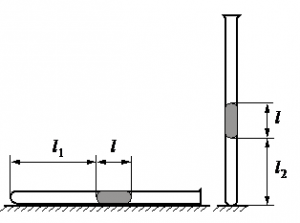 В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23,8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст. Температуру воздуха в трубке считать постоянной.
В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23,8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст. Температуру воздуха в трубке считать постоянной.