Заставить колебаться можно любую материю. Так, колебаться могут не только физические тела, состоящие из вещества, но и электромагнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между электрически заряженными частицами. Когда происходят колебания в механической системе, говорят, что тело совершает периодически повторяющиеся движения — оно отклоняется от положения равновесия то в одну, то в другую сторону. Когда происходят электромагнитные колебания, говорят, что электромагнитное поле периодически изменяется во времени, то есть его характеристики, то уменьшаются, то увеличиваются относительного некоторого среднего значения, которое является для них «положением равновесия».
Напомним, что напряженность E представляет собой количественную характеристику электромагнитного поля, а индукция B — силовую. Причем электромагнитное поле — это взаимосвязанные между собой электрическое и магнитные поля. Так, проводник с током создает вокруг себя магнитное поле. Оно тем сильнее, чем выше сила тока в этом проводнике, которая напрямую зависит от напряжения в нем (или количества заряда, прошедшего через него за единицу времени). Поэтому изменения напряжения и силы тока в проводнике вызывают изменения напряженности и индукции магнитного поля. Следовательно, можно сделать вывод, что:
Осциллограф
Но если колебания физических тел наблюдать легко, то колебания электромагнитного поля обнаружить без специальных приборов нельзя. Ведь увидеть изменения заряда, силы тока или напряжения невозможно. Использовать для этого электроизмерительные приборы (гальванометры, вольтметры или амперметры) тоже неудобно, поскольку электромагнитные колебания происходят с гораздо большей частотой по сравнению с механическими. Поэтому специально для визуализации электромагнитных колебаний был создан прибор, который называется осциллографом.

Осциллограф, схему которого вы видите ниже, представляет собой электронно-лучевую трубку. Через нее проходит узкий пучок электронов и попадает на экран, который начинает светиться при бомбардировке электронами.
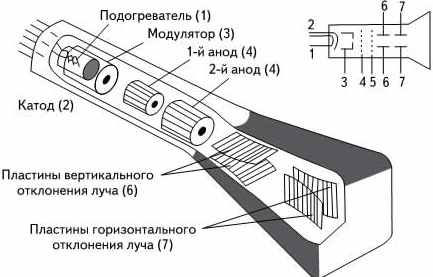
На горизонтально отклоненные пластины трубки подается переменное напряжение развертки up пилообразной формы (см. рисунок ниже). Оно медленно нарастает и быстро падает. Поэтому электрическое поле между пластинами заставляет электронный луч пробегать экран в горизонтальном направлении с постоянной скоростью и затем почти мгновенно возвращаться назад. После этого весь процесс повторяется.
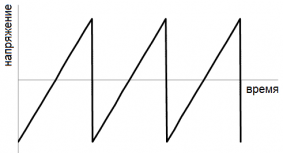
Если же присоединить вертикально отклоняющие пластины трубки к конденсатору, то колебания напряжения при его разрядке вызовут колебания луча в вертикальном направлении. В результате на экране осциллографа образуется временная развертка колебаний. Она напоминает синусоиду или косинусоиду подобно той, с помощью которой можно описать механические колебания.
С течением времени электромагнитные колебания затухают. Такие колебания являются свободными. Напомним, что свободными колебаниями называют такие колебания, которые возникают в колебательной системе после выведения ее из положения равновесия. В нашем случае система выводится из равновесия при сообщении конденсатору заряда. Зарядка конденсатора эквивалента отклонения математического маятника от положения равновесия.
В электрической цепи также можно получить вынужденные колебания, которые будут происходить до тех пор, пока на колебательную систему действует периодическая внешняя сила. Вынужденными электромагнитными колебаниями называют колебания в цепи под действием внешней периодической электродвижущей силы.
Колебательный контур
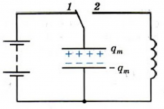
Колебательный контур состоит из конденсатора и катушки, присоединенной к его обкладкам (см. рисунок выше). Попробуем выяснить, почему в этом контуре возникают электромагнитные колебания. Для этого зарядим конденсатор, присоединив его на некоторое время к батарее с помощью переключателя (см. схему ниже).
При этом конденсатор получит энергию, равную:
Wp=q2max2C
где qmax — заряд конденсатора, а C — его электроемкость. Между обкладками конденсатора возникает разность потенциалов Umax.
Теперь переведем переключатель в положение 2 (см. схему ниже). После этого конденсатор начнет разряжаться, и в цепи появится электрический ток. Сила тока достигнет максимального значения не сразу, а будет увеличиваться постепенно. Это объясняется явлением самоиндукции. При появлении тока возникает переменное магнитное поле. Это переменное магнитное поле порождает вихревое электрическое поле в проводнике. Вихревое электрическое поле при возрастании магнитного поля действует против тока и препятствует его мгновенному увеличению.
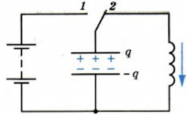
По мере разрядки конденсатора энергия электрического поля уменьшается, но одновременно возрастает энергия магнитного поля тока, которая определяется формулой:
Wм=Li22
где i — сила переменного тока, L — индуктивность катушки.
Полная энергия W электромагнитного контура равна сумме энергий магнитного и электрического полей:
W=Li22+q22C
В момент, когда конденсатор полностью разрядится (q = 0), энергия электрического поля станет равной нулю. Но согласно закону сохранения энергии, максимальное значение обретет энергия магнитного поля. Сила тока в этот момент примет максимальное значение Imax.
К этому моменту разность потенциалов на концах катушки становится равной нулю. Но, несмотря на это, электрический ток не может исчезнуть сразу. Этому снова препятствует явление самоиндукции. Как только сила тока и созданное им магнитное поле начнут уменьшаться, возникает вихревое электрическое поле, которое поддерживает ток.
Конденсатор будет перезаряжаться до тех пор, пока сила тока, постепенно уменьшаясь, не станет равной нулю. Энергия магнитного поля в этот момент тоже будет равна нулю, а энергия электрического поля конденсатора опять будет максимальной. После этого конденсатор снова начнет перезаряжаться, и система вернется в исходное состояние.
Из-за частичных потерь энергии электромагнитные колебания являются затухающими. Если бы потерь не было, полная энергия система была бы постоянной и была бы равной:
W=Li22+q22C=q2max2C=LI2max2
Пример №1. После того как конденсатору колебательного контура был сообщен заряд q = 10–5 Кл, в контуре возникли затухающие колебания. Какое количество теплоты выделится в контуре к тому времени, когда колебания в нем полностью затухнут? Емкость конденсатора C = 0,01 мкФ.
0,01 мкФ = 10–8 Ф
Поскольку с каждым колебанием колебательный контур теряет часть энергии в виде выделения тепла, ко времени, когда колебания полностью затухнут, выделится полная электромагнитная энергия системы. Ее можно определить формулой:
Сходство электромагнитных колебаний в контуре со свободными механическими колебаниями
Электромагнитные колебания в контуре имеют сходство со свободными механическими колебаниями (к примеру, колебаниями тела, закрепленного на пружине). Сходство относится не к природе самих величин, которые периодически изменяются, а к процессам периодического изменения различных величин.
Соответствие между механическими и электрическими величинами при колебательных процессах
| Механическая величина | Электрическая величина |
| Координата x | Заряд q |
| Скорость vx | Сила тока i |
| Масса m | Индуктивность L |
| Жесткость пружины | Величина, обратная емкости 1C |
| Потенциальная энергия растянутой пружины kx22 | Энергия электрического поля q22C |
| Кинетическая энергия mv2x2 | Энергия магнитного поля Li22 |
Уравнение, описывающее процессы в колебательном контуре
Рассмотрим колебательный контур, сопротивлением R которого можно пренебречь (см. схему ниже).
Полная электромагнитная энергия равна сумме энергий магнитного и электрического полей:
W=Li22+q22C
Если его сопротивление равно 0, то полная механическая энергия с течением времени не меняется. А производная константы равна нулю. Следовательно, сумма производных от каждой составляющей этой энергии также равна нулю.
(Li22)′+(q22C)′=0
Или:
(Li22)′=−(q22C)′
Первая производная по времени характеризует скорость изменения физической величины. Следовательно, эта формула позволяет сделать вывод о том, что скорость изменения энергии магнитного поля равна скорости изменения электрического поля. Знак «минус» указывает на то, что, когда энергия электрического поля возрастает, энергия магнитного поля уменьшается (и наоборот).
Вычислив обе производные, получим:
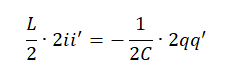
Но производная заряда по времени представляет собой силу тока в данный момент времени:
i=limΔt→0ΔqΔt=q′
Поэтому мы можем записать уравнение иначе:
Lii′=−qiC
Производная силы тока по времени представляет собой вторую производную заряда по времени:
i′=q
″
Подставив это равенство в уравнение, и преобразовав его путем деления на величину Li, получим основное уравнение, описывающее свободные электрические колебания в контуре:
q″=−1LCq
Формула Томсона
Когда мы рассматривали механические колебания, то вводили величину, постоянную для конкретной колебательной системы — коэффициент km. Он представляет собой квадрат собственной частоты колебаний. По аналогии в случае с электромагнитными колебаниями этот коэффициент равен 1LC. Он также представляет собой квадрат циклической частоты свободных электрических колебаний:
ω0=1√LC
Следовательно, период свободных колебаний в контуре равен:
T=2πω0=2π√LC
Эта формула называется формулой Томсона.
Пример №2. Колебательный контур состоит из катушки индуктивностью L = 0,003 Гн и плоского конденсатора емкостью C = 13,4 пФ. Определите период свободных колебаний в контуре.
13,4 пФ = 13,4∙10–12 Ф
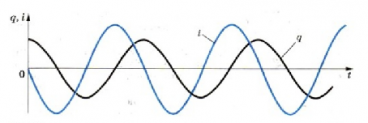
Гармонические колебания заряда и тока
Заряд конденсатора меняется с течением времени подобно тому, как координата при механических колебаниях изменяется со временем по гармоническому закону (в случае, когда в начальный момент времени отклонение от положения равновесия максимально):
q=qmaxcosω0t
где qmax — амплитуда колебаний заряда.
Сила тока также совершает гармонические колебания:
i=q‘=−ω0qmaxsinω0t=Imaxcos(ω0t+π2)
где Imax — амплитуда колебаний силы тока, равная произведению циклической частоты на амплитуду колебаний заряда:
Imax=qmax ω0
Колебания силы тока опережают по фазе на π2 колебания заряда, что хорошо видно на рисунке ниже.
Пример №3. В двух идеальных колебательных контурах с одинаковой индуктивностью происходят свободные электромагнитные колебания, причём период колебаний в первом контуре 9⋅10−8 с, во втором 3⋅10−8 с. Во сколько раз амплитудное значение силы тока во втором контуре больше, чем в первом, если максимальный заряд конденсаторов в обоих случаях одинаков?
Максимальная сила тока равна:
Imax=qmax ω0
Так как максимальный заряд конденсаторов одинаков в обоих контурах, отношение силы тока во тором контуре к силе ток в первом контуре равно:
I2 maxI1 max=qmaxω02 qmaxω01=ω02 ω01
Циклическую частоту выразим из формулы Томсона:
ω0=2πT
Тогда:
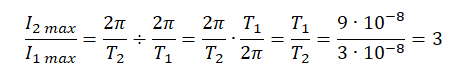
Автоколебания
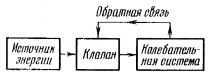
Незатухающие вынужденные колебания поддерживаются в цепи действием внешнего периодического напряжения. Но существует способ создания незатухающих колебаний, при котором колебательная система сама регулирует поступление энергии в колебательный контур для компенсации потерь энергии на резисторе.
Самый простой пример автоколебательной системы — это генератор на транзисторе. Транзистор представляет собой полупроводниковое устройство, состоящее из эмиттера, базы и коллектора и имеющее 2 p–n перехода. Колебания тока в контуре вызывают колебания напряжения между эмиттером и базой, которые, в свою очередь, управляют силой тока в цепи колебательного контура (обратная связь). От источника напряжения в контур поступает энергия, компенсирующая потери энергии в контуре на транзисторе.
Схема автоколебательной системы представлена ниже.
Преимуществом такой схемы является то, что конденсатор при этом подключается к источнику тока только тогда, когда присоединенная к положительному источнику тока пластина конденсатора заряжена положительно (рис. а). Только в этом случае конденсатор восполняет потери энергии, выделенной на резисторе.
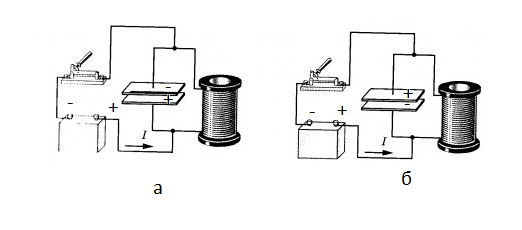
Если бы источник тока был включен всегда, восполнения потерь не происходило бы. Поскольку конденсатор разряжался бы в момент, когда он соединен с источником тока пластиной, заряженной отрицательно (рис. б).
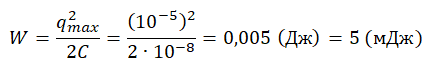
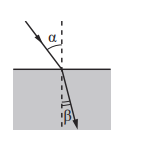 Плоская световая волна переходит из воздуха в глицерин (см. рисунок). Что происходит при этом переходе с периодом электромагнитных колебаний в световой волне и с длиной волны?
Для каждой величины определите соответствующий характер изменения:
Плоская световая волна переходит из воздуха в глицерин (см. рисунок). Что происходит при этом переходе с периодом электромагнитных колебаний в световой волне и с длиной волны?
Для каждой величины определите соответствующий характер изменения:

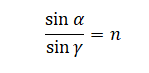
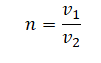
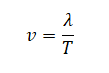

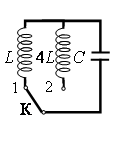 Как изменится период собственных электромагнитных колебаний в контуре (см. рисунок), если ключ К перевести из положения 1 в положение 2?
Как изменится период собственных электромагнитных колебаний в контуре (см. рисунок), если ключ К перевести из положения 1 в положение 2?