Сила Лоренца | теория по физике 🧲 магнетизм

Определение

Сила Лоренца — сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.

Модуль силы Лоренца обозначается как F_Л. Единица измерения — Ньютон (Н).

Модуль силы Лоренца численно равен отношению модуля силы F, действующий на участок проводника длиной l, к числу N заряженных частиц, упорядоченно движущихся на этом участке проводника:

$F_{Л} = \frac{F}{N}$

Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка ∆l и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля $\to B$ можно считать неизменным в пределах этого отрезка проводника.

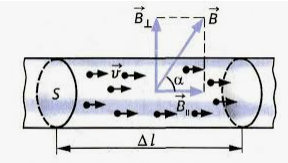
Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (число зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:

$I = q n v S$

Модуль силы, действующей со стороны магнитного поля на выбранные элемент тока, равен:

$F = | I | Δ l B sin . α$

Подставляя сюда выражение, полученное для силы тока, получим:

$F = | q n v S | Δ l B sin . α = | q | n v S Δ l B sin . α$

Учтем, что число заряженных частиц в рассматриваемом объеме равно произведению величины этого объема на концентрацию самих частиц:

$N = n S Δ l B$

Тогда:

$F = | q | v N B sin . α$

Следовательно, на каждый движущийся заряд действует сила Лоренца, равная:

$F_{Л} = \frac{F}{N} = \frac{| q | v N B sin . α}{N} = | q | v B sin . α$

α — угол между вектором скорости движущегося заряда и вектором магнитной индукции.

Пример №1. Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45^o к вектору магнитной индукции.

$F_{Л} = | q | v B sin . α = 0, 005 \cdot 200 \cdot 0, 3 \cdot \frac{\sqrt{2}}{2} \approx 0, 2 (Н)$

Направление силы Лоренца

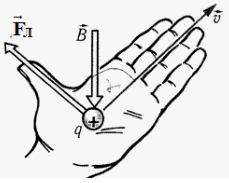
Сила Лоренца перпендикулярна вектору магнитной индукции и вектору скорости движущегося заряда. Ее направление определяется с помощью правила левой руки:

Если левую руку расположить так, чтобы составляющая магнитной индукции $\to B$ , перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца.

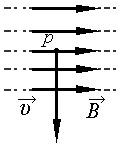
Пример №2. Протон p имеет скорость $\to v$ , направленную горизонтально вдоль прямого длинного проводника с током I (см. рисунок). Куда направлена действующая на протон сила Лоренца?

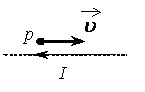
В точке, в которой находится протон, вектор магнитной индукции направлен в сторону от наблюдателя. Это следует из правила буравчика. Теперь применим правило левой руки. Для этого четыре пальца левой руки направим в сторону движения протона — вправо. Ладонь развернем в сторону наблюдателя, чтобы линии магнитной индукции входили в нее перпендикулярно. Теперь отставим на 90 градусов большой палец. Он показывает вверх. Следовательно, сила Лоренца, действующая на протон, направлена вверх.

Работа силы Лоренца

Поскольку вектор силы Лоренца направлен перпендикулярно скорости движения заряда, угол между перемещением этого заряда и этой силы равен 90^о. Работа любой силы определяется формулой:

$A = F s cos . α$

Но так как косинус 90^о равен 0, сила Лоренца не совершает работу. Это значит, что сила Лоренца не влияет на модуль скорости перемещения заряда. Но она может менять вектора его скорости.

Полная сила, действующая на заряд

При решении задач, в которых заряженная частица находится одновременно в электрическом и магнитном полях, нужно учитывать, что не нее действует сразу две силы. Со стороны магнитного поля — сила Лоренца. Со стороны электрического поля — сила ${\to F}_{э л}$ , действующая на неподвижный заряд, помещенный в данную точку поля. Она равна произведению этого заряда на напряженность электрического поля:

${\to F}_{э л} = q \to E$

Следовательно, полная сила, действующая на заряд, равна:

$\to F = {\to F}_{э л} + {\to F}_{л} = q \to E + | q | \to v \to B sin . α$

Пример №3. В пространстве, где существует одновременно однородное и постоянное электрическое и магнитное поля, по прямолинейной траектории движется протон. Известно, что напряженность электрического поля равна $\to E$ . Какова индукция $\to B$ магнитного поля?

Прямолинейное движение протона возможно в двух случаях:

Вектор $\to E$ направлен вдоль траектории движения протона. Тогда вектор $\to B$ также должен быть направлен вдоль этой траектории, и его модуль может быть любым, так как магнитное поле на частицу действовать не будет.
Векторы $\to E$ , $\to B$ и $\to v$ взаимно перпендикулярны, и сила, действующая на протон со стороны электрического поля, равна по модулю и противоположна по направлению силе Лоренца, действующей на протон со стороны магнитного поля (см. рисунок).

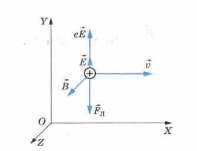
Заряд протона равен модулю заряда электрона — $e$ . Сложим силы, действующие на протон по оси ОУ:

$e \to E + {\to F}_{Л} = 0$

В скалярной форме:

$e E - e v B = 0$

Следовательно:

$B = \frac{E}{v}$

Текст: Алиса Никитина, 9.2k 👀

Задание ЕГЭ-Ф-ДВ2023-13

Две частицы с зарядами q₁ = 2q и q₂ = q влетают в однородное магнитное поле перпендикулярно вектору магнитной индукции со скоростями υ₁ = υ и υ₂ = 2υ соответственно. Определите отношение модулей сил F₁ : F₂, действующих на них со стороны магнитного поля.

Алгоритм решения:

Записать исходные данные.
Записать формулу для определения силы, действующей со стороны магнитного поля на движущуюся в нем заряженную частицу.
Найти отношение модуля силы, действующей на 1 заряд, к модулю силу, действующей на второй заряд.

Решение:

Запишем исходные данные:

Заряд первой частицы: q₁ = 2q.
Заряд второй частицы: q₂ = q.
Скорость первой частицы: υ₁ = υ.
Скорость второй частицы: υ₂ = 2υ.

На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца, модуль которой равен:

Угол α — это угол между векторами скорости и магнитной индукции. Так как частицы влетают перпендикулярно векторам магнитной индукции, синус этого угла равен 1. Следовательно, применительно к данному случаю, можем применять формулу:

Сила Лоренца, действующая на частицу 1, равна:

Сила Лоренца, действующая на частицу 2, равна:

Найдем отношение первой силы ко второй:

Ответ: 1

pазбирался: Алиса Никитина | обсудить разбор

Задание ЕГЭ-Ф-ДВ2023-20

Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.

При увеличении длины нити математического маятника период его колебаний уменьшается.
Явление диффузии протекает в твёрдых телах значительно медленнее, чем в жидкостях.
Сила Лоренца отклоняет положительно и отрицательно заряженные частицы, влетающие под углом к линиям индукции однородного магнитного поля, в противоположные стороны.
Дифракция рентгеновских лучей невозможна.
В процессе фотоэффекта с поверхности вещества под действием падающего света вылетают электроны.

Алгоритм решения:

1.Установить, как период колебаний изменяется с изменением длины математического маятника.

2.Установить, как зависит скорость протекания диффузии от агрегатного состояния вещества.

3.Установить, как действует сила Лоренца на заряженные частицы, которые влетают под углом к линиям индукции однородного магнитного поля.

4.Установить, возможна ли дифракция рентгеновских лучей.

5.Установить, как ведут себя электроны в процессе фотоэффекта.

6.Выбрать только верные утверждения и записать цифры, под которыми они располагаются, в порядке возрастания.

Решение:

Период колебаний математического маятника определяется формулой:

Видно, что период колебаний прямо пропорционален корню из длины нити математического маятника. Следовательно, с уменьшением длины нити период колебаний уменьшается. Получается, утверждение 1 неверно.

Явление диффузии характерно для веществ, находящихся в любых агрегатных состояниях. Оно протекает тем быстрее, чем больше расстояние между молекулами вещества. Следовательно, быстрее всего диффузия протекает в газах, медленнее — в жидкостях. Медленнее всего она протекает в твердых телах. Поэтому утверждение 2 верное.

Чтобы проверить 3 утверждение, вспомним правило левой руки, по которому можно определить направление силы Лоренца. Оно звучит следующим образом:

Если левую руку расположить так, чтобы вектор индукции магнитного поля входил в ладонь, четыре вытянутых пальца указывали направление скорости движения положительно заряженной частицы (или против движения отрицательного), тогда отогнутый на 90 градусов большой палец в плоскости ладони укажет направление силы Лоренца.

Если же направление силы Лоренца известно, но неизвестно, куда будет направлена скорость движения заряженной частицы, можем изменить это правило так:

Если левую руку расположить так, чтобы вектор индукции магнитного поля входил в ладонь, а отогнутый на 90 градусов большой палец в плоскости ладони указывал направление силы Лоренца, то четыре вытянутых пальца будут указывать направление скорости движения положительно заряженной частицы (или направление, обратно направлению движения отрицательной частицы).

Отсюда видно, что сила Лоренца действует на заряженные частицы по-разному — положительно заряженные частицы направляются в одну сторону, а отрицательно заряженные — в противоположную ей. Следовательно, утверждение 3 верно.

Дифракция — явление отклонения волн от их прямолинейного распространения. Оно характерно для любых волн, в том числе рентгеновских. Следовательно, утверждение 4 неверно.

Чтобы установить истинность 5 утверждения, нужно вспомнить лишь определение фотоэффекта:

Фотоэффект — это испускание электронов из вещества под действием падающего на него света.

Из определения видно, что действительно — под действием падающего света с поверхности вещества вылетают электроны. Следовательно, утверждение 5 верно.

Правильная последовательность цифр в ответе — 235.

Ответ: 235

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17621

Протон ускоряется постоянным электрическим полем конденсатора, напряжение на обкладках которого 2160 В. Затем он влетает в однородное магнитное поле и движется по дуге окружности радиуса 20 см в плоскости, перпендикулярной линиям магнитной индукции. Каков модуль вектора индукции магнитного поля? Начальной скоростью протона в электрическом поле пренебречь. Ответ выразить в мТл, округлив до десятых.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Записать формулу для определения силы Лоренца.

3.Выразить модуль вектора магнитной индукции.

4.Определить недостающие величины.

5.Выполнить решение в общем виде.

6.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Напряжение на обкладках конденсатора: U = 2160 В.

• Радиус окружности, по которой движется протон в однородном магнитном поле: R = 20 см.

• Масса протона: m = 1,673·10^–27 кг.

• Заряд протона: q = 1,6·10^–19 Кл.

20 см = 0,2 м

Сила Лоренца определяется формулой:

$F_{Л} = | q | v B sin . α$

По условию задачи протон движется перпендикулярно вектору магнитной индукции. Поэтому синус угла между вектором скорости и вектором магнитной индукции будет равен 1. А протон имеет положительный заряд. Тогда:

$F_{Л} = q v B$

Сила Лоренца сообщает протону центростремительное ускорение, равное:

$a = \frac{v^{2}}{R}$

Применим второй закон Ньютона:

$F = m a$

$q v B = \frac{m v^{2}}{R}$

Отсюда модуль вектора магнитной индукции равен:

$B = \frac{m v^{2}}{q v R} = \frac{m v}{q R}$

Энергия заряда, движущегося в электрическом поле, определяется формулой:

$W = q U$

Но энергию заряда также можно выразить как кинетическую энергию движения:

$W = E_{к} = \frac{m v^{2}}{2}$

Приравняем правые части выражений и получим:

$q U = \frac{m v^{2}}{2}$

Отсюда ускорение протона равно:

$v = \sqrt{\frac{2 q U}{m}}$

Конечная формула для определения модуля вектора магнитной индукции:

$B = \frac{m v}{q R} = \frac{m}{q R} \sqrt{\frac{2 q U}{m}} = \sqrt{\frac{2 U m}{q R^{2}}}$

Ответ: 33,6

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17600

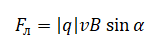
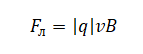
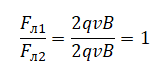
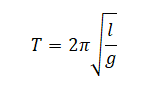
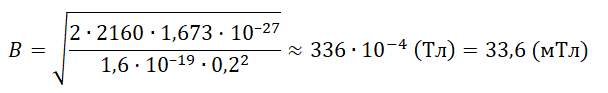
Протон движется в однородном магнитном поле со скоростью υ, направленной перпендикулярно вектору магнитной индукции B (см. рисунок). Как направлена сила Лоренца, действующая на протон?

а) влево

б) вправо

в) к нам

г) от нас

Алгоритм решения

Определить, каким способом можно найти направлений силы Лоренца, действующей на протон.
Применить правила и найти направление силы Лоренца.

Решение

Силу Лоренца, действующую на заряженную частицу, можно найти с помощью правила левой руки. Для этого мысленно расположим четыре пальца левой руки в сторону, совпадающей с направлением движения положительной частицы (протона). Относительно рисунка пальца будут направлены вниз. Теперь развернем ладонь так, чтобы в нее входили линии магнитной индукции. Теперь отклоним на 90 градусов большой палец. Он будет направлен от плоскости рисунка к нам. Это и есть направление силы Лоренца, действующей на протон.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17749

Протон в однородном магнитном поле движется по окружности. Чтобы в этом поле двигалась по окружности с той же скоростью α-частица, радиус окружности, частота обращения и энергия α-частицы по сравнению с протоном должны:

увеличиться
уменьшиться
не измениться

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

1.Записать формулу для определения силы Лоренца.

2.Установить, от чего зависят перечисленные в таблице физические величины.

3.Определить характер их изменения при изменении заряда.

Решение

Сила Лоренца определяется формулой:

$F_{Л} = | q | v B sin . α$

Если вместо протона взять альфа-частицу, то заряд увеличится вдвое, так как альфа-частица содержит 2 протона. Сила Лоренца прямо пропорционально зависит от величины заряда. Следовательно, она тоже увеличится вдвое. Скорость движения заряда по условию задачи остается постоянной, как и модуль вектора магнитной индукции.

Сила Лоренца будет сообщать альфа-частице центростремительное ускорение, равное:

$a = \frac{v^{2}}{R}$

Применим второй закон Ньютона:

$F = m a$

$| q | v B sin . α = \frac{m v^{2}}{R}$

Отсюда:

$| q | B sin . α = \frac{m v}{R}$

$R = \frac{m v}{| q | B sin . α}$

Заряд альфа-частицы больше заряда протона вдвое. Она также содержит 2 нейтрона, поэтому ее масса примерно в 4 раза больше массы протона. Следовательно, радиус движения альфа-частицы увеличится примерно вдвое.

Частота обращения альфа-частицы связана с ее линейной скоростью формулой:

$v = 2 π R ν$

Так как скорость остается постоянной, то при увеличении радиуса частота обращения должна уменьшиться.

Энергия альфа-частицы будет больше, чем у протона, вращающегося с той же скоростью. Это связано с тем, что ее кинетическая энергия будет примерно в 4 раза больше (так как во столько раз больше ее масса).

Ответ: 121

pазбирался: Алиса Никитина | обсудить разбор

ЕГЭ по физике

Вся теория

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

Направление силы Лоренца

Работа силы Лоренца

Полная сила, действующая на заряд

Задание ЕГЭ-Ф-ДВ2023-13

Задание ЕГЭ-Ф-ДВ2023-20

Задание EF17621

Задание EF17600

Задание EF17749

ЕГЭ по физике

Вся теория

Добавить комментарий Отменить ответ