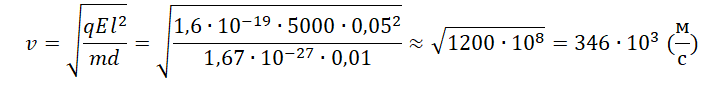Конденсаторы | СПАДИЛО

Определение

Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.

Плоский конденсатор — система двух разноименно заряженных пластин.

Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:

$U = E d$

Электроемкость конденсатора

Определение

Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.

Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).

Электроемкость конденсатора определяется формулой:

$C = \frac{ε_{0} ε S}{d}$

$ε_{0}$ — диэлектрическая постоянная, равная 8,85∙10^–12 Кл²/(Н∙м²);
$ε$ — диэлектрическая проницаемость среды;
$S$ (м²) — площадь каждой пластины.

Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.

Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:

$C = \frac{Q}{U} = \frac{q}{U}$

Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.

Энергия конденсатора

Формула энергии конденсатора

Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:

$W_{э} = \frac{q^{2}}{2 C} = \frac{C U^{2}}{2}$

Подсказки к задачам

Конденсатор отключен от источника	q = q′
Конденсатор подключен к источнику	U = U′
Количество теплоты и энергия конденсатора	Q = ∆W_э

Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.

10 см = 0,1 м

1 мм = 0,001 м

Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.

Площадь квадратной пластины равна квадрату ее стороны:

S = a²

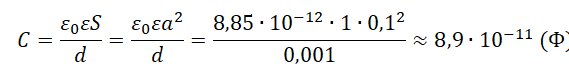
Соединения конденсаторов

	Последовательное соединение	Параллельное соединение
Схема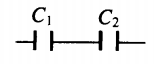
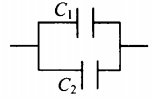Напряжение	$U = U_{1} + U_{2}$	$U = U_{1} = U_{2}$
Заряд	$q = q_{1} = q_{2}$	$q = q_{1} + q_{2}$
Электроемкость	$\frac{1}{C} = \frac{1}{C_{1}} + \frac{1}{C_{2}}$	$C = C_{1} + C_{2}$

Подсказки к задачам

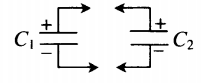
Два конденсатора, электроемкости которых C₁и C₂, заряжены до напряжения U₁и U₂. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами.

Схема соединения конденсаторов одноименными полюсами:

Заряд системы после соединения:

${q'} = C_{1} U_{1} + C_{2} U_{2}$

Электрическая емкость системы:

${C'} = C_{1} + C_{2}$

Напряжение:

${U'} = \frac{q^{'}}{C'} = \frac{C_{1} U_{1} + C_{2} U_{2}}{C_{1} + C_{2}}$

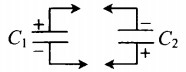
Два конденсатора, электроемкости которых C₁и C₂, заряжены до напряжения U₁и U₂. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами.

Схема соединения конденсаторов разноименными полюсами:

Заряд системы после соединения:

${q'} = C_{1} U_{1} - C_{2} U_{2}$

Электрическая емкость системы:

${C'} = C_{1} + C_{2}$

Напряжение:

${U'} = \frac{q^{'}}{C'} = \frac{C_{1} U_{1} - C_{2} U_{2}}{C_{1} + C_{2}}$

Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.

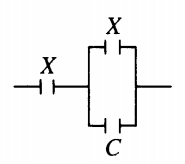
Электрическая емкость параллельного соединения равна:

$C_{п а р а л} = X + C$

Электроемкость последовательного соединения:

$\frac{1}{C_{п о с л е д}} = \frac{1}{C_{п а р а л}} + \frac{1}{X} = \frac{1}{X + C} + \frac{1}{X}$

Учтем, что суммарная электроемкость равна C:

$\frac{1}{C} = \frac{1}{X + C} + \frac{1}{X}$

Преобразуем, умножим выражение на CX(X+C):

$X (X + C) = C X + C (X + C)$

Раскроем скобки:

$X^{2} + X C = C X + C X + C^{2}$

$X^{2} - C X - C^{2} = 0$

Решив уравнение, получим: X = 25,9 пФ.

Разбор задач на тему «Заряженная частица в поле конденсатора»

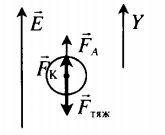
Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρ_ш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U?	Условие равновесия исходит из второго закона Ньютона: ${- F}_{т я ж} + {- F}_{K} + {- F}_{A} = 0$ ρ_ш > ρ, поэтому ${- F}_{т я ж}$ > ${- F}_{A}$ . В этом случае сила Кулона направлена вверх, а заряд шарика положительный. Схематически это можно отобразить так: Проекция второго закона Ньютона на ось ОУ: $F_{K} + F_{A} = F_{т я ж}$ Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения: $F_{т я ж} = ρ_{ш} \frac{4}{3} π r^{3} g$ Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения: $F_{А} = ρ \frac{4}{3} π r^{3} g$ Сила Кулона: $F_{K} = \frac{q U}{d}$ $\frac{q U}{d} + ρ \frac{4}{3} π r^{3} g = ρ_{ш} \frac{4}{3} π r^{3} g$ $q = {(ρ}_{ш} \frac{4}{3} π r^{3} g - ρ \frac{4}{3} π r^{3} g) \frac{d}{U} = \frac{4 π r^{3} g d (ρ_{ш} - ρ)}{3 U}$
Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l?	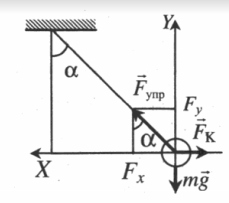Условие равновесия исходит из второго закона Ньютона: ${- F}_{т я ж} + {- F}_{K} + {- F}_{у п р} = 0$ Проекции на оси ОХ и ОУ соответственно: $F_{у п р} sin . α - F_{K} = 0$ $F_{у п р} cos . α - m g = 0$ Отсюда: $k Δ l sin . α = \frac{q U}{d}$ $k Δ l cos . α = m g$ Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их: ${(k Δ l)}^{2} {sin}^{2} . α + {(k Δ l)}^{2} {cos}^{2} . α = {(\frac{q U}{d})}^{2} + {(m g)}^{2}$ ${(k Δ l)}^{2} ({sin}^{2} . α + {cos}^{2} . α) = {(\frac{q U}{d})}^{2} + {(m g)}^{2}$ ${sin}^{2} . α + {cos}^{2} . α = 1$ ${(k Δ l)}^{2} = {(\frac{q U}{d})}^{2} + {(m g)}^{2}$ $U = \frac{d}{q} \sqrt{{(k Δ l)}^{2} - {(m g)}^{2}}$
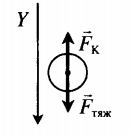
Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь.	Второй закон Ньютона в векторной форме: ${- F}_{т я ж} + {- F}_{K} = 0$ Проекция на вертикальную ось: $F_{т я ж} - F_{K} = 0$ $F_{т я ж} = m g$ $F_{K} = \frac{q U}{d}$ $m g = \frac{q U}{d}$ $d = \frac{q U}{m g}$
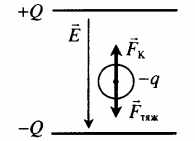
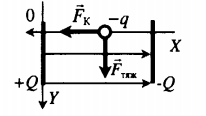
Между двумя параллельными горизонтально расположенными диэлектрическими пластинами создано однородное электрическое поле с напряженностью $- E,$ направленное вертикально вниз. Между пластинами помещен шарик на расстоянии d от верхней пластины и b от нижней. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени t шарик ударится об одну из пластин, если система находится в поле силы тяжести Земли?	Второй закон Ньютона в векторной форме: ${- F}_{т я ж} + {- F}_{K} = m - a$ Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок: Если F_тяж> F_K, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны: $a = \frac{m g - q E}{m}$ $s = b$ Если F_тяж< F_K, то шарик движется с ускорением верх. Ускорение и перемещение в этом случае равны: $a = \frac{q E - m g}{m}$ $s = d$ Начальная скорость шарика равна нулю. Поэтому перемещение также равно: $s = \frac{a t^{2}}{2}$ Сделаем вычисления для случая F_тяж> F_K: $\frac{a t^{2}}{2} = b$ $\frac{m g - q E}{m} \frac{t^{2}}{2} = b$ $t = \sqrt{\frac{2 b m}{m g - q E}}$ Выполняя вычисления для случая Сделаем вычисления для случая F_тяж< F_K, получим: $t = \sqrt{\frac{2 b m}{q E - m g}}$
Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого $- E$ и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер.	Второй закон Ньютона в векторной форме: ${- F}_{т я ж} + {- F}_{K} = m - a$ Если сила Кулона направлена вправо, то s_x = d. Если сила Кулона направлена вправо, то s_x = b. Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево. Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно: $a_{x} = \frac{q E}{m}$ $a_{y} = g$ Проекции перемещений на эти же оси: $s_{x} = \frac{a_{x} t^{2}}{2}$ $s_{x} = Δ h = \frac{g t^{2}}{2}$ $\frac{a_{x} t^{2}}{2} = b$ Или: $\frac{q E}{m} \frac{t^{2}}{2} = b$ Так как время движения шарика по вертикали и горизонтали одинаково: $t^{2} = \frac{2 Δ h}{g} = \frac{2 m b}{q E}$ $Δ h = \frac{m b g}{q E}$

Задание EF17979

Введите ответ в поле ввода Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?

Для каждой величины определите соответствующий характер изменения:

увеличится
уменьшится
не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

1.Определить, от чего зависит емкость конденсатора, и как она изменится при уменьшении зазора между его обкладками.

2.Определить, от чего зависит величина заряда конденсатора, и как она изменится после уменьшения зазора между его обкладками.

3.Определить, от чего зависит разность потенциалов между обкладками конденсатора, и как она изменится при уменьшении зазора.

Решение

Емкость конденсатора определяется формулой:

$C = \frac{ε_{0} ε S}{d}$

Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.

Вот как взаимосвязана электроемкость и заряд конденсатора:

$C = \frac{q}{U}$

Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.

С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.

Ответ: 113

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18574

Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.

Алгоритм решения

1.Проанализировать каждый этап эксперимента.

2.Установить, от чего зависит угол отклонения стрелки электрометра.

3.Выяснить, что поменяется при смещении одной пластины конденсатора относительно другой, и что при этом произойдет со стрелкой электрометра.

Решение

На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.

На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:

$C = \frac{ε_{0} ε S}{d}$

S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.

Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.

На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:

$C = \frac{q}{U}$

Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.

Ответ: Увеличатся

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18695

Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?

Алгоритм решения

Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.

Решение

Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18703

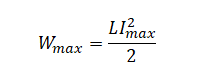
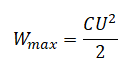
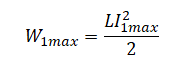
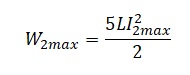
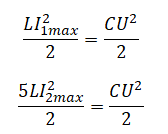
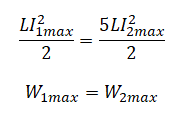
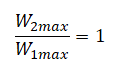
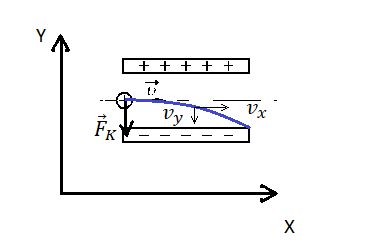
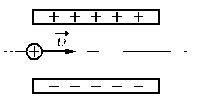Протон влетает в электрическое поле конденсатора параллельно его пластинам в точке, находящейся посередине между пластинами (см. рисунок). Найдите минимальную скорость $υ,$ с которой протон должен влететь в конденсатор, чтобы затем вылететь из него. Длина пластин конденсатора 5 см, расстояние между пластинами 1 см, напряжённость электрического поля конденсатора 5000 В/м. Поле внутри конденсатора считать однородным, силой тяжести пренебречь.

Ответ записать в км/с, округлив до десятков.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Выполнить рисунок. Указать направление движения протона и силы, действующие на него.

3.Выяснить, при каком условии протон успеет вылететь из конденсатора.

4.Выполнить решение в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса протона: m = 1,67∙10^–27 кг.

• Заряд протона: q = 1,6∙10^–19 Кл.

• Расстояние между обкладками конденсатора: d = 1 см.

• Длина пластин конденсатора: l = 5 см.

• Напряженность однородного поля внутри конденсатора: E = 5000 В/м.

1 см = 0,01 м

5 см = 0,05 м

Сделаем рисунок:

Изначально протон обладает только горизонтальной скоростью v, равной v_x. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.

Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью v_x:

$t = \frac{l}{v_{x}} = \frac{l}{v}$

Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):

$0, 5 d = \frac{a t^{2}}{2}$

Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:

$t = \sqrt{\frac{d}{a}}$

Приравняем правые части уравнений времени и получим:

$\frac{l}{v} = \sqrt{\frac{d}{a}}$

Отсюда скорость равна:

$v = \sqrt{\frac{a l^{2}}{d}}$

Ускорение выразим из второго закона Ньютона:

$F_{K} = m a = \frac{q U}{d}$

$a = \frac{q U}{m d}$

Но известно, что:

$U = E d$

Поэтому:

$a = \frac{q E d}{m d} = \frac{q E}{m}$

Отсюда:

Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙10³ м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.

Ответ: 350

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 5.1k

Конденсаторы | теория по физике 🧲 электростатика

Электроемкость конденсатора

Энергия конденсатора

Подсказки к задачам

Соединения конденсаторов

Подсказки к задачам

Разбор задач на тему «Заряженная частица в поле конденсатора»

Добавить комментарий Отменить ответ