В опытах с резиновым шнуром и шариками, соединенными пружиной, мы наблюдали волны, которые распространялись только в одну сторону. В сплошных средах волны распространяются по всем направлениям. Сплошной средой можно считать любую жидкость, газ или твердой тело, которые сплошь заполняют некоторую область пространства.
В сплошной среде волны всегда являются затухающими. Это связано с тем, что при колебательном движении между частицами возникают силы трения. Поэтому полная механическая энергия колеблющихся частиц уменьшается. Вспомним, что полная механическая энергия колеблющегося тела равна:
W=kx2max2
где xmax — амплитуда колебаний, а k — коэффициент упругости.
Поскольку часть энергии уходит на преодолении сил трения, со временем она уменьшается. Следовательно, уменьшается и амплитуда колебаний частиц. Исключение составляют плоские волны, амплитуда колебаний которых остается постоянной (или почти постоянной).
Плоские волны
Все частицы, лежащие в одной плоскости, параллельной пластине, колеблются в одной фазе. Поверхности равной фазы называются волновыми поверхностями. А линию, перпендикулярную такой поверхности, называют лучом. Под направлением распространения волн понимают направление лучей.
Волновые поверхности плоской волны представляют собой плоскости, параллельные колеблющейся пластине.
При распространении плоской волны размеры волновых поверхностей по мере удаления от пластины не меняются (или почти не меняются). Поэтому энергия волны не рассеивается в пространстве, и амплитуда колебаний уменьшается только за счет действия сил трения.
Сферические волны
Другой пример волны в среде — сферическая волна. Сферическая волна возникает, если в среду поместить пульсирующую сферу. В этом случае волновые поверхности представляют собой сферы. Лучи же направляются вдоль продолжений радиусов пульсирующей сферы (см. рисунок).
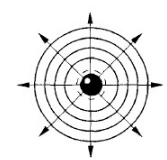
Амплитуда колебаний частиц в случае сферической волны обязательно убывает по мере удаления от источника. Энергия, излучаемая источником, в этом случае равномерно распределяется по поверхности сферы, радиус которой непрерывно увеличивается по мере распространения волны.
Площадь поверхности сферы пропорциональна квадрату радиуса:
S=4πr2
Следовательно, энергия, переносимая волной, убывает обратно пропорционально квадрату расстояния от источника:
W~1r2
Амплитуда же колебаний, квадрат которой пропорционален энергии, убывает обратно пропорционально первой степени расстояния от источника:
smax~1r
Пример №1. Найти расстояние между точками пространства 1 и 2, если известно, что в точке 1 энергия волны равна 10 Дж, а в точке 2— 6 Дж. Считать, что в среде нет трения.
Поскольку энергия волны убывает обратно пропорционально квадрату расстояния от источника, примем, что разность энергий волны в точках 1 и 2 обратно пропорциональна квадрату расстояния между ними:
(W1−W2)~1r2
(10−6)~1r2
4~1r2
Тогда:
r~√14~12 (м)
Поперечные и продольные волны в средах
Как вы знаете, волны могут быть поперечными и продольными. В поперечной волне смещения отдельных участков среды происходят в направлении, перпендикулярном распространению волны. При этом происходит упругая деформация, называемая деформацией сдвига. Отдельные слои вещества сдвигаются друг относительно друга. Объем тела не изменяется. При деформации сдвига в твердом теле возникают силы упругости, стремящиеся вернуть тело в исходное состояние. Именно эти силы и вызывают колебания среды.
Сдвиг слоев друг относительно друга в газах и жидкостях не приводит к появлению сил упругости. Поэтому в газах и жидкостях не могут существовать поперечные волны. Поперечные волны возникают только в твердых телах.
В продольной волне происходит деформация сжатия и растяжения. Силы упругости, связанные с этой деформацией, возникают как в твердых телах, так и в жидкостях и газах. Эти силы вызывают колебания отдельных участков среды, поэтому продольные волны могут распространяться во всех средах.
Звуковые волны
Волны на поверхности воды или волны вдоль резинового шнура можно непосредственно видеть. В прозрачной среде — воздухе или жидкости — волны невидимы. Но при определенных условиях их можно слышать.
Зажмем в тиски металлическую линейку и отклоним ее верхнюю часть в сторону, затем отпустим. Линейка начнет совершать колебательные движения. Мы их увидим, но не услышим.
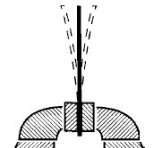
Теперь проделаем тот же самый опыт, но укоротим линейку. Теперь мы сможем не только видеть, но и слышать колебания.
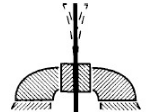
Почему одни колебания можно услышать, а другие нет? Все дело в частоте колебаний. В опытах линейка совершала колебания разных частот. Известно, что период колебаний зависит от длины колеблющегося тела. Он пропорционален корню из этой длины:
T~√l
Следовательно, когда длина линейки меньше, период колебаний тоже меньше. Также известно, что период представляет собой величину, обратную частоте:
T=1ν
Следовательно, если период колебаний меньше, то частоты выше. Ухо человека воспринимает колебания сплошных сред как звук, если их частота находится в диапазоне от 16 до 20 000 Гц.
Пример №2. Сильный ветер раскачивает ствол дерева так, что он совершает одно колебание за 2 секунды. Определить, услышит ли человек звук раскачивающегося ствола дерева.
Чтобы дать ответ на вопрос, нужно найти частоту колебаний дерева:
ν=1T=12 (Гц)
Теперь сравним полученное значение с частотами, которые может слышать человек. Минимальная частота, воспринимаемая человеческим ухом, составляет 16 Гц. 1/2 меньше 16. Следовательно, звук колебаний ствола дерева человек не услышит.
Как возбуждаются звуковые волны
Как же получается, что мы можем слышать звук колеблющегося конца линейки? Дело в том, что когда линейка отклоняется, она толкает воздух впереди себя, создавая уплотнение. С обратной же стороны образуется разрешение. То есть, колеблющаяся линейка порождает продольную волну.
Так как воздух — сплошная среда, то волна распространяется во все стороны. Она состоит из чередующихся зон повышенной и пониженной плотности (см. рисунок ниже). Плотные участки воздуха давят на барабанную перепонку уха. Так волна становится слышимой.
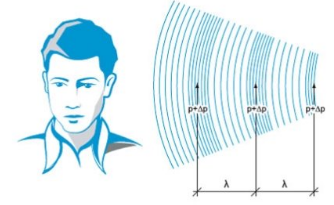
Звук может распространяться в любой среде: жидкой, газообразной и твердой. Причем чем плотнее среда, тем быстрее распространяется звук. Так, быстрее всего звуковая волна распространяется в твердых телах, чуть медленнее — в жидкостях. Медленнее всего она распространяется в воздухе. В вакууме звук услышать нельзя. Звук представляет собой продольную волну в сплошной вещественной среде. В вакууме вещества нет (или почти нет).
Скорость звука
Звуковые волны, подобно всем другим волнам, распространяются с конечной скоростью. Обнаружить это можно так. Свет распространяется с огромной скоростью — 300 000 км/с. Поэтому вспышка от выстрела почти мгновенно достигает глаз. Звук же выстрела приходит с заметным запаздыванием. То же самое можно заметить, наблюдая с большого расстояния игру в футбол. Вы видите удар по мячу, а звук от удара приходит спустя некоторое время. Все, вероятно, замечали, что вспышка молнии предшествует раскату грома. Если гроза далеко, то запаздывание грома достигает нескольких десятков секунд. Наконец, из-за конечной скорости звука появляется эхо. Эхо — это звуковая волна, отраженная от опушки леса, крутого берега, здания и т. д.
Чтобы вычислить скорость звука, нужно знать расстояние от источника звука до слушателя, а также разницу времени между тем, как звук был издан, и тем, как он был услышан. В таком случае скорость можно будет вычислить по формуле:
v=st
Так как звук — это волна, то скорость звука является скорость распространения волны, которая равна отношению длины волны к периоду колебаний:
v=λT
Приведем в таблице приблизительные скорости звука в различных средах.
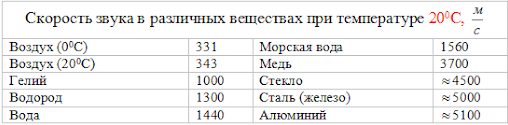
Пример №3. Определите скорость звука в воде, если колебания с периодом T = 0,005 с, порождают звуковую волну длиной λ = 7,175 м.
v=λT=7,175 0,005=1435 (мс)
Эхо
Звуковые волны, распространяющихся в неплотных средах (например, в воздухе), имеют способность отражаться от более плотных сред (твердых тел) в направлении к источнику звука. Эхо можно услышать в горах, в лесу, в большом пустом помещении, но его нельзя услышать в маленькой комнате. С чес же это связано?
Человеческое ухо воспринимает одинаковые звуки как два отдельных звука только в случае, если временной между ними составляет не менее 0,06 с. Если отраженная звуковая волна достигла уха раньше, чем за это время, мозг объединит эти звуки в один. Чем меньше расстояние от источника звука до препятствия, тем быстрее приходит эхо.
Пример №4. Это, вызванное ружейным выстрелом, дошло до стрелка через 4 с после выстрела. На каком расстоянии от наблюдателя находится преграда, от которой произошло отражение звука? Считать, что скорость звука в воздухе равна 330 м/с.
Звуковая волна прошла двойное расстояние от стрелка до препятствия: сначала от наблюдателя к этому препятствию, затем от препятствия к этому наблюдателю. Следовательно, найти его можно по следующей формуле:
2s=vt
s=vt2=330·42=660 (м)