Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:
Пример №1. Кислород находится в сосуде вместимостью 0,4 м3 под давлением 8,3∙105 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.
Из основного уравнения состояния идеального газа выразим массу:
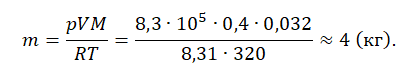
Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.
Подсказки к задачам
| Давление возросло на 15% | p2 = 1,15p1 |
| Объем увеличился на 2% | V2 = 1,02V1 |
| Масса увеличилась в 3 раза | m2 = 3m1 |
| Газ нагрелся до 25 оС | T2 = 25 + 273 = 298 (К) |
| Температура уменьшилась на 15 К (15 оС) | T2 = T1 – 15 |
| Температура уменьшилась в 2 раза | |
| Масса уменьшилась на 20% | m2 = 0,8m1 |
| Выпущено 0,7 начальной массы |
Важна только та масса, что осталась в сосуде. Поэтому: m2 = 0,3m1 |
| Какую массу следует удалить из баллона? | Нужно найти разность начальной и конечной массы:
m1 – m2 |
| Газ потерял половину молекул | |
| Молекулы двухатомного газа (например, водорода), диссоциируют на атомы | |
| Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ) | M (O3) = 3Ar (O)∙10–3 кг/моль
M (O2) = 2Ar (O)∙10–3 кг/моль |
| Открытый сосуд | Объем V и атмосферное давление pатм остаются постоянными |
| Закрытый сосуд | Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины |
| Нормальные условия | Температура T0 = 273 К
Давление p0 = 105 Па |
| Единицы измерения давления | 1 атм = 105 Па |
Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.
2,8 МПа = 2,8∙106 Па
1,5 МПа = 1,5∙106 Па
Так как половина молекул была выпущена, m2 = 0,5m1. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:
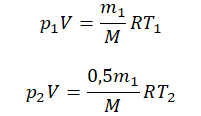
Преобразим уравнения и получим:
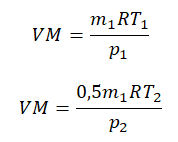
Приравняем правые части и выразим искомую величину:
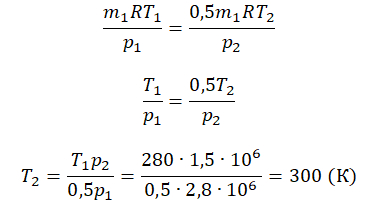
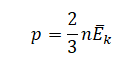
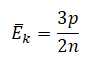
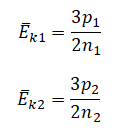
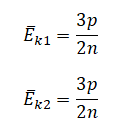

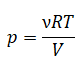
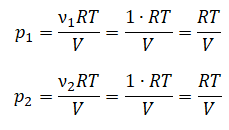
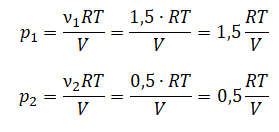

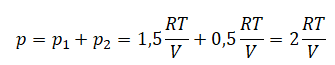
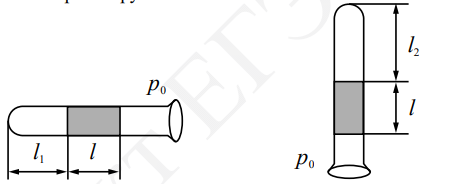
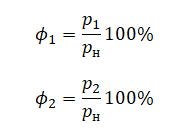
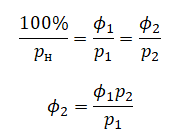

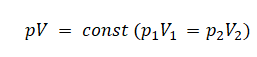
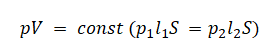
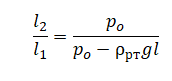
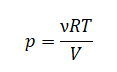
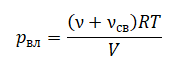
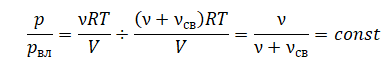
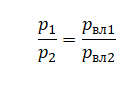
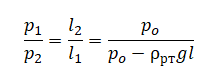
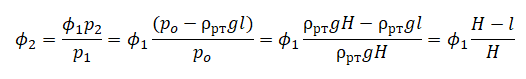
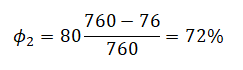
 На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.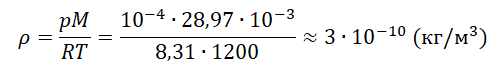
 Одноатомный идеальный газ в количестве ν моль помещают в открытый сверху сосуд под лёгкий подвижный поршень и начинают нагревать. Начальный объём газа V0, давление p0. Масса газа в сосуде остаётся неизменной. Трением между поршнем и стенками сосуда пренебречь. R
Одноатомный идеальный газ в количестве ν моль помещают в открытый сверху сосуд под лёгкий подвижный поршень и начинают нагревать. Начальный объём газа V0, давление p0. Масса газа в сосуде остаётся неизменной. Трением между поршнем и стенками сосуда пренебречь. R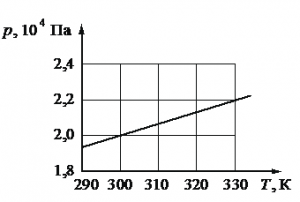 На рисунке показан график зависимости давления газа в запаянном сосуде от его температуры. Объём сосуда равен 0,25 м3. Какое приблизительно количество газообразного вещества содержится в этом сосуде? Ответ округлите до целых.
На рисунке показан график зависимости давления газа в запаянном сосуде от его температуры. Объём сосуда равен 0,25 м3. Какое приблизительно количество газообразного вещества содержится в этом сосуде? Ответ округлите до целых.
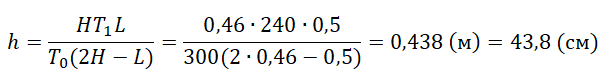
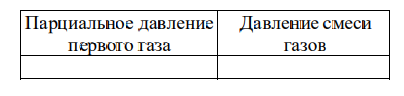
 В сосуде неизменного объёма при комнатной температуре находилась смесь неона и аргона, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль аргона. Как изменились в результате парциальное давление неона и давление смеси газов, если температура газов в сосуде поддерживалась неизменной?
В сосуде неизменного объёма при комнатной температуре находилась смесь неона и аргона, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль аргона. Как изменились в результате парциальное давление неона и давление смеси газов, если температура газов в сосуде поддерживалась неизменной?