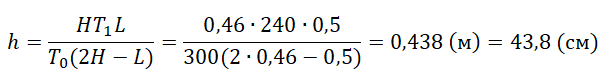Задание EF18093 • СПАДИЛО

В камере, заполненной азотом, при температуре К находится открытый цилиндрический сосуд (см. рис. 1). Высота сосуда см. Сосуд плотно закрывают цилиндрической пробкой и охлаждают до температуры К. В результате расстояние от дна сосуда до низа пробки становится равным h (см. рис. 2). Затем сосуд нагревают до первоначальной температуры T₀. Расстояние от дна сосуда до низа пробки при этой температуре становится равным см (см. рис. 3). Чему равно h? Величину силы трения между пробкой и стенками сосуда считать одинаковой при движении пробки вниз и вверх. Массой пробки пренебречь.

📜Теория для решения: Уравнение состояния идеального газа

Посмотреть решение

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения физических величин в СИ.

2.Записать уравнение Менделеева — Клапейрона и применить его ко всем состояниям газа.

3.Определить условие равновесия пробки.

4.Выполнить решение задачи в общем виде.

5.Вычислить искомую величину.

Решение

Запишем исходные данные:

• Начальная температура азота: T₀ = 300 К.

• Высота сосуда: L = 50 см.

• Температура азота после охлаждения: T₁ = 240 К.

• Высота столба азота после нагревания: H = 46 см.

50 см = 0,5 м

46 см = 0,46 м

Запишем уравнение Менделеева — Клапейрона:

$p V = ν R T$

Так как количество азота не меняется, можем принять, что:

$\frac{p V}{T} = c o n s t$

Применим уравнение Менделеева — Клапейрона для всех трех состояний азота. Учтем, что

$\frac{p_{0} V_{0}}{T_{0}} = \frac{p_{1} V_{1}}{T_{1}} = \frac{p_{2} V_{2}}{T_{2}}$

Пусть S — площадь поперечного сечения сосуда. Тогда объемы столба азота для каждого из состояний будут равны:

$V_{0} = S L$

$V_{1} = S h$

$V_{2} = S H$

Известно, что в состоянии 3 температура азота поднимается до первоначальной. Поэтому уравнение Менделеева — Клапейрона примет вид:

$\frac{p_{0} S L}{T_{0}} = \frac{p_{1} S h}{T_{1}} = \frac{p_{2} S H}{T_{0}}$

$\frac{p_{0} L}{T_{0}} = \frac{p_{1} h}{T_{1}} = \frac{p_{2} H}{T_{0}}$

Неизвестными остались только давления. Их можно определить, записав условие равновесия пробки.

В состоянии 1 сила давления азота на пробку определяется формулой:

$p_{0} S = p_{а т м} S$

В состоянии 2 на пробку действует сила давления со стороны азота и атмосферного давления, я а также сила трения, направленная вверх. Следовательно:

$p_{1} S = p_{а т м} S - F_{т р} = p_{0} S - F_{т р}$

В состоянии 3 на пробку действуют те же силы, но сила трения теперь действует не вверх, а вниз. Поэтому:

$p_{2} S = p_{а т м} S + F_{т р} = p_{0} S + F_{т р}$

Выразим из этих уравнений силу трения:

$F_{т р} = p_{0} S - p_{1} S$

$F_{т р} = p_{2} S - p_{0} S$

Приравняем правые части и получим:

$p_{0} S - p_{1} S = p_{2} S - p_{0} S$

Отсюда:

$p_{0} - p_{1} = p_{2} - p_{0}$

${2 p}_{0} = p_{2} + p_{1}$

$p_{0} = \frac{p_{2} + p_{1}}{2}$

Подставим это значение в уравнение Менделеева — Клапейрона и получим:

$\frac{\frac{p_{2} + p_{1}}{2} L}{T_{0}} = \frac{p_{1} h}{T_{1}} = \frac{p_{2} H}{T_{0}}$

Отсюда:

$\frac{p_{2} + p_{1}}{2} L = p_{2} H$

$p_{2} L + p_{1} L = {2 p}_{2} H$

$p_{1} L = {2 p}_{2} H - p_{2} L = p_{2} (2 H - L)$

$p_{1} = \frac{p_{2} (2 H - L)}{L}$

Отсюда:

$\frac{\frac{p_{2} (2 H - L)}{L} h}{T_{1}} = \frac{p_{2} H}{T_{0}}$

Давление слева и справа взаимоуничтожается. Остается:

$\frac{T_{0} (2 H - L)}{L} h = H T_{1}$

Отсюда выразим h:

Текст: Алиса Никитина, 1k 👀