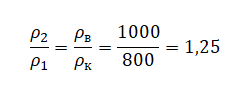Задание Статика 5
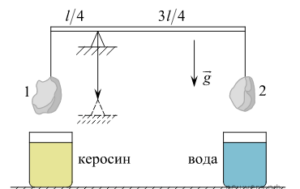К концам лёгкого стержня длиной l, лежащего на клиновидной опоре, установленной на расстоянии 
от его левого конца, подвешены на невесомых нитях два тяжёлых груза 1 и 2 с плотностями 
(слева) и 
(справа). Стержень находится в равновесии в горизонтальном положении (см. рис.).
Затем, опустив точку опоры стержня, грузы полностью погрузили в стаканы с жидкостями — керосином слева и водой справа, опустив точку опоры стержня, и при этом его равновесие сохранилось. Чему равно отношение плотностей грузов 
Какие законы Вы использовали для решения этой задачи? Обоснуйте их применимость к данному случаю. 📜Теория для решения: Момент силы и правило моментов Правило моментов при решении задач Давление твердого тела Давление в жидкостях и газах. Закон Паскаля. Сообщающиеся сосуды Архимедова сила
Посмотреть решение
Алгоритм решения:
Решение:
Запишем исходные данные:
Нет необходимости переводить единицы измерения в СИ.
Будем считать, что система тел находится в инерциальной системе отсчета. Условимся, что все тела в ней неподвижные, а стержень жесткий, тела при погружении в жидкости не касаются дна и стенок сосудов. Поэтому можем использовать законы статики и гидростатики — условия равновесия твердого тела в инерциальной системе отсчета и закон Архимеда. Так как нити по условию невесомые, будем считать, что сила натяжения в каждой точке одинакова.
Введём инерциальную систему отсчёта — далее в ней будем рассматривать проекции всех сил на вертикальную ось, так как сил, направленных по горизонтали, не наблюдается.
Стержень в обоих случаях является неподвижным, поэтому моменты сил натяжения нитей слева и справа от точки опоры направлены противоположно и одинаковы:
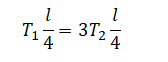
Отсюда следует:
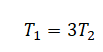
На каждый из тел действует сила тяжести (направлена вниз) и сила натяжения нити (направлена вверх). Когда тела опускаются в жидкости, на них дополнительно действует сила Архимеда, которая направлена вверх.
Составим условия равновесия для тел 1 и 2 в момент, когда они не были погружены в жидкости:
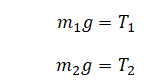
Или (выразим массу через плотность и объем, а силу натяжения 1 выразим через силу натяжения 2):
Подставим 2 выражение в 1:
Преобразовываем:
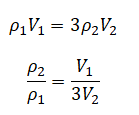
Теперь составим условие равновесия для второго случая. При этом силы натяжения нити будут уменьшены. Но так как система остается в равновесии, их соотношение останется прежним и будет равно:
Сами условия равновесия для тел 1 и 2 после погружения следующие:
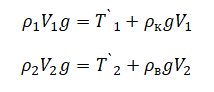
Преобразуем 1 выражение:
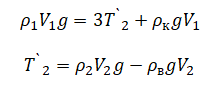
Подставим 2 выражение в 1:
Преобразуем:
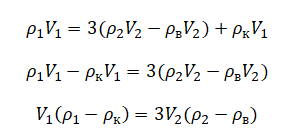
Но выше мы уже нашли, что:
Вычтем из этого выражения предыдущее и получим:
Отсюда:
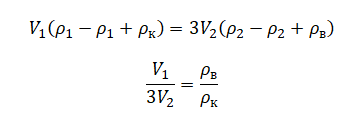
Выше уже получили, что:
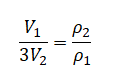
Следовательно:
