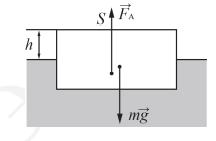
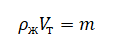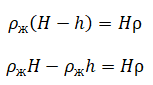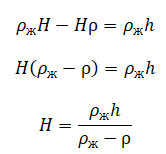Такая особенность передача давления жидкостями и газами связана с подвижностью молекул в жидком и газообразном состояниях.
Давление столба жидкости определяется формулой:
p = ρжgh
p — давление столба жидкости (Па), ρж — плотность жидкости (кг/м3), g — ускорение свободного падения (≈10 м/с2), h — высота столба жидкости, или ее глубина (м).
Важно! Высоту h нужно определять от поверхности жидкости.
Сила давления жидкости
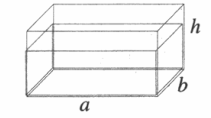
Сила давления жидкости на дно сосуда — это произведение давления, оказываемого жидкостью на дно сосуда, на площадь этого дна:
F = pS = ρжghab
Сила давления жидкости на боковую грань сосуда — это произведение половины давления, оказываемого жидкостью на дно сосуда, на площадь грани:
F=ρжgh2hb
Подсказки к задачам:
- Плотность пресной воды равна 1000 кг/м3.
- Плотность соленой воды равна 1030 кг/м3.
Пример №1. Чему равно давление, созданное водой, на глубине 2 м?
Давление в жидкостях определяется формулой:
p = ρжgh.
Давление, созданное пресной водой, равно:
p = 1000∙10∙2 = 20000 (Па) = 20 (кПа)
Давление, созданное соленой водой, равно:
p = 1030∙10∙2 = 20600 (Па) = 20,6 (кПа)
Гидростатический парадокс
Из закона Паскаля следует, что давление на дно сосуда определяется только плотностью жидкости и высотой ее столба. Поэтому, если в разные сосуды налить одинаковую жидкость одинаковой высоты, давление, оказываемое ею на дно каждого из сосудов, будет одинаковым.
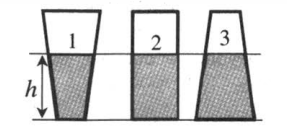
p1 = p2 = p3
Сила давления при этом будет разная, так как она прямо пропорционально зависит от площади дна. Так как площадь дна первого сосуда минимальна, а третьего максимальна, силы давления, оказываемые жидкостью на дно сосудов, будут такими:
F1 < F2 < F3
Пример №2. На рисунке изображены три сосуда с разными жидкостями. Площади дна сосудов равны. В первом сосуде находится вода (ρ1 = 1 г/см3), во втором — керосин (ρ2 = 0,8 г/см3), в третьем — спирт (ρ3 = 0,8 г/см3). В каком сосуде оказывается максимальное давление на дно?
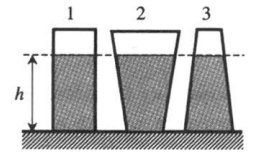
Давление зависит только от плотности жидкости и от ее столба: площадь сосудов никакой роли не играет. Так как столбы жидкостей во всех сосудах одинаково, остается сравнивать плотности. Плотность воды больше плотности керосина и плотности спирта. Поэтому в сосуде 1 давление на дно сосуда будет максимальным.