Относительность механического движения | теория по физике 🧲 кинематика

Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.

Относительность перемещения

Пусть движение материальной точки (МТ) описывается относительно двух систем отсчета: подвижной (ПСО) и неподвижной (НСО). Зная, как эта точка движется относительно ПСО, и, как ПСО движется относительно НСО, можно вычислить перемещение точки относительно НСО. В этом заключается правило сложения перемещений:

s′ = s₁ + s₂

s′ — перемещение МТ относительно НСО, s₁— перемещение МТ относительно ПСО, s₂ — перемещение ПСО относительно НСО.

Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.

Полезные факты

• Если тело движется в направлении движения ПСО, то модуль его перемещения относительно НСО равен сумме модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:

s′ = s₁ + s₂

• Если тело движется противоположно движению ПСО, то модуль его перемещения относительно НСО равен разности модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:

s′ = s₁ – s₂

• Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его перемещения относительно НСО равен корню из суммы квадратов перемещений этого тела относительно ПСО и перемещения ПСО относительно НСО:

s′ = √(s₁² + s₂²)

• Если относительно ПСО тело покоится, то его перемещение относительно НСО равно перемещению ПСО относительно НСО: при s₁=0, перемещение s′ = s₂
• Если тело движется относительно двух НСО, то его перемещение относительно НСО₁ равно перемещению движения относительно НСО₂. В этом случае одну из систем можно принять за ПСО с нулевой скоростью. Тогда ее перемещение относительно НСО будет равно 0. При s₂=0, перемещение s′ = s₁

Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.

Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:

s′=|s₁ – s₂|=|10 – 2|=8 (м).

Относительность скорости в ПСО и НСО

Тела и системы отсчета могут двигаться с различной скоростью. Но, зная скорость движения МТ относительно ПСО и скорость движения ПСО относительно НСО, можно вычислить скорость движения МТ относительно НСО. В этом заключается правило сложения скоростей:

v′ = v + u

v′ — скорость МТ относительно НСО, v — скорость МТ относительно ПСО, u — скорость движения ПСО относительно НСО.

Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.

Полезные факты

• Если тело движется в направлении движения ПСО, то модуль его скорости относительно НСО равен сумме модулей скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

v′ = v + u

• Если тело движется противоположно движению ПСО, то модуль его скорости относительно НСО равен разности модуля скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

v′ = v – u

• Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его скорости относительно НСО равен корню из суммы квадратов скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

v′ = √(v² + u²)

• Если относительно ПСО тело покоится, то его скорость относительно НСО равна скорости ПСО относительно НСО: при v=0, скорость v′ = u
• Если тело движется относительно двух НСО, то его скорость относительно НСО1 равна скорости движения относительно НСО2. В этом случае одну из неподвижных систем можно принять за ПСО с нулевой скоростью. При u=0, скорость v′ = u

Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.

Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.

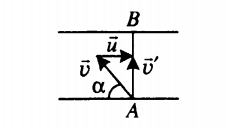
Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:

Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):

Косинусу 0,5 соответствует угол, равный 60 градусам.

Относительная скорость двух тел

Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.

Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:

v_отн = v₁– v₂

v_отн — относительная скорость, или скорость первого тела относительно второго, v₁ и v₂ — скорость первого и второго тела относительно СО.

Варианты обозначения относительной скорости и их проекций:

• v₁₂ — скорость первого тела относительно второго. Ее проекция равна:

v_12x = v_1x – v_2x

• v₂₁ — скорость второго тела относительно первого. Ее проекция равна v_21x = v_2x – v_1x

Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.

Полезные факты

• Если тела движутся в одном направлении, то относительная скорость равна модулю разности скоростей первого и второго тела:

v_отн = |v₁ – v₂|

• Если тела движутся в противоположных направлениях, то относительная скорость равна сумме скоростей первого и второго тела:

v_отн = |v₁ + v₂|

• Если тела движутся взаимно перпендикулярно, то относительная скорость равна корню из суммы квадратов скоростей первого и второго тела:

v_отн = √(v₁² + v₂²)

Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.

Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:

Скорость второго автомобиля относительно дороги равна 80 км/час.

Правила сложения векторов

Эта таблица иллюстрирует правила сложения векторов на примере векторов a и b. Результатом их сложения является вектор c .

Сложение двух сонаправленных векторов
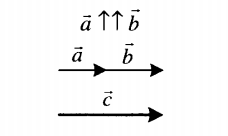	Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону. Его длина равна сумме длин слагаемых векторов: c = a + b.
Сложение двух противоположно направленных векторов
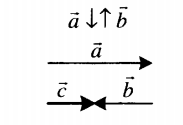	Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|.
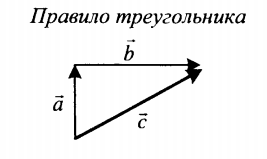
Сложение двух векторов, расположенных друг к другу под углом
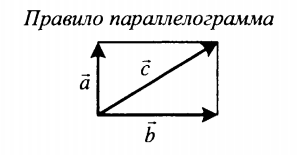
Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
	Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора: .
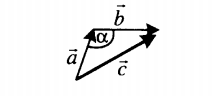	Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .
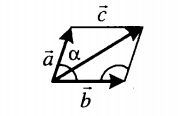	Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .

Правила вычитания векторов

Эта таблица иллюстрирует правила вычитания векторов на примере векторов Результатом их вычитания является вектор .

Вычитание двух сонаправленных векторов
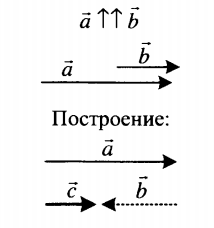	Разностью двух сонаправленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин вычитаемых векторов: c = |a – b|.
Вычитание двух противоположно направленных векторов
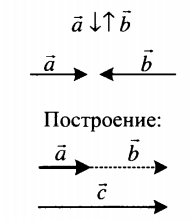	Разность двух противоположно направленных векторов есть вектор, направленный в сторону уменьшаемого вектора. Его длина равна сумме длин вычитаемых векторов: c = a + b.
Вычитание двух векторов, расположенных друг к другу под углом
Разностью двух векторов, расположенных друг к другу под углом является вектор, являющийся обратным вектору, образующемуся при сложении этих векторов. Его направление определяется графически. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
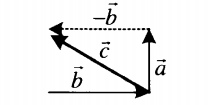	Если вычитаемые векторы перпендикулярны, для вычисления длины вектора их разности используется теорема Пифагора: .
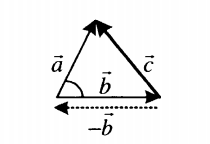	Если вычитаемые векторы расположены под углом α, для вычисления длины вектора их разности используется теорема косинусов: .

Алиса Никитина | Просмотров: 7.1k