Задание EF19015

Алгоритм решения

Решение

Запишем исходные данные:

Выполним рисунок. Проведем перпендикуляры к поверхности: перпендикуляр от точечного источника света, а также нормали, проведенные через края плота.

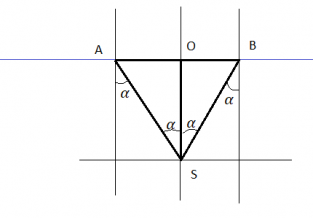
Чтобы свет лампочки не выходил из воды, лучи света от лампочки, направленные к границе между краем плота и поверхностью воды, должны полностью отражаться. Это возможно только при выполнении следующего условия:

$\sin .\alpha =\frac{1}{n}$

Поскольку вершина S треугольника ABS лежит строго под центром круглого плота, этот треугольник является равнобедренным. Причем перпендикуляр, восстановленный к основанию треугольника AB — SO — делит это основание на 2 равные стороны. Одновременно он делит угол S этого треугольника на 2 равные части, так как он является одновременно перпендикуляром, медианой и биссектрисой.

Пусть $\alpha$ — угол падения луча. Тогда угол OSB будет равен этому углу как накрест лежащие углы.

Треугольник OSB — прямоугольный. Причем искомая величина — глубина бассейна — является одним из его катетов. Из курса геометрии известно, что катет равен произведения второго катета на котангенс прилежащего угла. Второй катет в нашем случае — радиус круглого плота. Прилежащий угол равен углу падения. Следовательно:

$H=R\cot .\alpha$

Котангенс угла определяется как отношение косинуса этого угла к его синусу:

$\cot .\alpha =\frac{\cos .\alpha }{\sin .\alpha }$

Косинус угла можем выразить из основного тригонометрического тождества:

${\sin }^2.\alpha +{\cos }^2.\alpha =1$

Следовательно:

$\cos .\alpha =\sqrt{1-{\sin }^2.\alpha }$

Отсюда котангенс равен:

$\cot .\alpha =\frac{\sqrt{1-{\sin }^2.\alpha }}{\sin .\alpha }$

Тогда глубина бассейна:

$H=R\cot .\alpha =R\frac{\sqrt{1-{\sin }^2.\alpha }}{\sin .\alpha }$

Из закона полного отражения вспомним, что синус угла падения есть величина, обратная показателю преломления воды. Тогда эта формула примет вид:

$H=R\frac{\sqrt{1-{\left(\frac{1}{n}\right)}^2}}{\frac{1}{n}}=Rn\sqrt{1-\frac{1}{n^2}}$

Подставим известные данные и получим:

$H=2,4·\frac{4}{3}\sqrt{1-\frac{1}{{\left(\frac{4}{3}\right)}^2}}=3,2\sqrt{1-\frac{9}{16}}=3,2\frac{\sqrt{7}}{4}\approx 0,8·2,65=2,12\left(м\right)$

.