Задание EF19112

Алгоритм решения

Решение

Запишем исходные данные:

10 см = 0,1 м

15 см = 0,15 м

Выполним рисунок. Для его построения достаточно найти изображение точки А. Затем в противоположную сторону отложим перпендикуляр и на таком же расстоянии от главной оптической оси будет находиться изображение точки B.

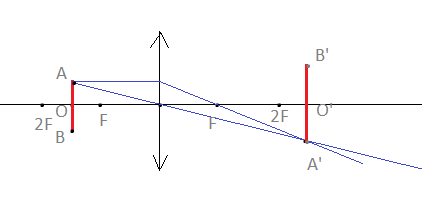
Глядя со стороны, мы будем видеть вместо окружности, которую описывает точка, линию AB. Она равн диаметру окружности, по которой движется точка. Обозначим ее радиус OA за r. Изображением окружности будет окружность. Вместо нее мы со стороны также увидим отрезок — A´B´. Обозначим радиус O´A´ за R.

Запишем формулу тонкой линзы и выразим из нее расстояние от изображения до линзы:

$\frac{1}{d}+\frac{1}{f}=\frac{1}{F}$

$\frac{1}{f}=\frac{1}{F}-\frac{1}{d}=\frac{d-F}{Fd}$

$f=\frac{dF}{d-F}$

Формулу линейного увеличения линзы можно определить как отношение радиуса окружности, по которой движется точка-изображение, к радиусу окружности, по которой движется сама точка:

$\Gamma =\frac{R}{r}$

.

Линейное увеличение также определяется формулой:

$\Gamma =\frac{f}{d}$

Следовательно:

$\frac{R}{r}=\frac{f}{d}$

Подставим сюда выражение, найденное для расстояния от изображения до линзы из формулы тонкой линзы:

$\frac{R}{r}=\frac{dF}{d\left(d-F\right)}=\frac{F}{d-F}$

Так как изображение будет двигаться вслед за точкой, то угловые скорости этой точки и изображения будут равны. Поэтому:

$\omega =\frac{v}{r}=\frac{V}{R}$

Отсюда линейная скорость движения изображения равна:

$V=\frac{Rv}{r}=\frac{Fv}{d-F}=\frac{0,1·5}{0,15-0,1}=10\left(\frac{м}{с}\right)$