Задание OM2601o
📜Теория для решения:
Посмотреть решение
Алгоритм решения:
- Делаем чертеж.
- Определяем равенство угла между касательной и хордой и угла АВС.
- Определяем соотношение отрезков из свойства биссектрисы угла треугольника и найдем АВ.
- Показываем, что треугольники DAC и DCB подобны.
- Составляем соотношения сторон подобных треугольников.
- Составляем систему равенств.
- Решаем систему.
- Записываем ответ.
Решение:
1. Выполняем чертеж данной задачи:
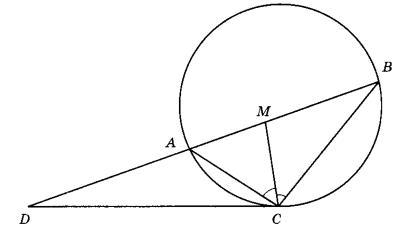
2. Рассматриваем АСD. В нем:
Согласно свойству углов окружности, касательной и секущей, угол, который образован этими линиями, равен половине градусной меры дуги, заключенной между сторонами этого угла. ∠DСА равен половине градусной меры дуги АС, заключенной между его сторонами СD и СА.
Но вписанный ∠СВА опирается на ту же дугу АС и по свойству вписанного угла равен половине меры этой дуги. Следовательно, ∠ СВА=∠ АСD.
3. Согласно свойству биссектрисы угла треугольника, она делит АВ на отрезки АМ и МВ, пропорциональные сторонам АС и ВС. Таким образом,
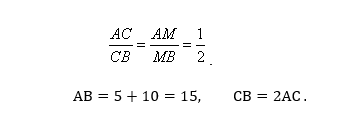
4. Рассмотрим DAC и DCB. У них:
∠ DCA = ∠ DBC по доказанному выше,
∠ D – общий.
Следовательно, DAC DCB по двум углам.
5. Из определения и свойств подобных треугольников имеем:
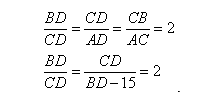
6. Составим систему равенств:
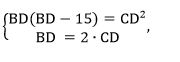
7. Решим систему:
