Задание OM2604o • СПАДИЛО

Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC . Найдите радиус окружности, вписанной в треугольник ABC .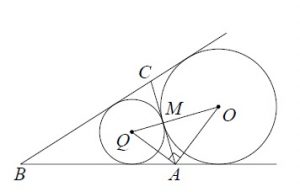

📜Теория для решения:

Посмотреть решение

Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC .

Точка касания M окружностей делит AC пополам по условию.

Лучи AQ и AO — биссектрисы смежных углов, так как касательные к окружностям равноудалены от центра. Так как AQ и AO — биссектрисы смежных углов, то угол OAQ прямой — смежные углы в сумме дают 180°, значит сумма их биссектрис:

180°/2 = 90°.

Далее рассмотрим прямоугольный треугольник OAQ. По свойству высоты в прямоугольном треугольнике, получаем:

AM² = MQ•MO

Отсюда:

QM = AM² / MO

QM = 6² / 8 = 4,5

Ответ: 4,5

Текст: Базанов Даниил, 544 👀