Задание OM2603o
ОГЭ▿высокий уровень сложности▿другое(архив)
Точки М и N лежат на стороне АС треугольника ABC на расстояниях соответственно 9 и 11 от вершины А. Найдите радиус окружности, проходящей через точки М и N и касающейся луча АВ, если cos ∠BAC = √11 / 6
📜Теория для решения:
📜Теория для решения:
Посмотреть решение
Алгоритм решения:
- Сделаем чертеж.
- Установим подобие треугольников AFM и ANF.
- Определим сторону FM.
- Определим ∠FNA.
- Найдем .
- Составим теорему синусов и найдем радиус окружности.
- Запишем ответ.
Решение:
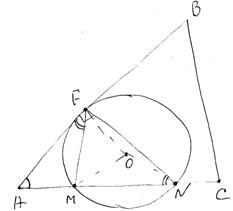
1. Рассмотрим треугольники AFM и ANF. У них:
Угол A является общим, а
![]() по доказанному выше.
по доказанному выше.
Следовательно, треугольник AFM подобен треугольнику ANF по двум углам. Отсюда вытекает:
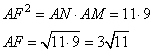
3. В треугольнике AFM сторона AF=3, сторона AM=9. Воспользуемся теоремой косинусов для определения FM:
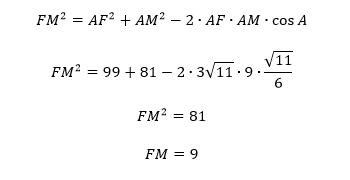
Полученное значение означает, что AFM является равнобедренным. У него основание AF.
4. По свойству равнобедренного треугольника ∠FAM=∠AFM. Отсюда
![]()
5. Найдем
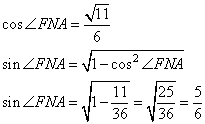
Значит,
![]()
6. Из FMN по теореме синусов:
![]()
где R – радиус описанной окружности.
Отсюда получим значение радиуса окружности:
![]()
Текст: Базанов Даниил, 516 👀
Подписаться
авторизуйтесь
Пожалуйста, войдите, чтобы прокомментировать
0 комментариев