Задание 22OM21R
ОГЭ▿базовый уровень сложности▿ОГЭ 2021()
Постройте график функции:
📜Теория для решения:
у=х2 - |2x +1|
Определите, при каких значениях m прямая у= m имеет с графиком ровно три общие точки.📜Теория для решения:
Посмотреть решение
Раскроем модуль:
{у=х2−2х−1, при х≥−12у=х2+2х+1, при х<−12)
Для построения графика найдем вершины каждой параболы:
у=х2 – 2х – 1
х0=−b2a=22=1
у0=12 -2-1=-2
Итак, вершина первой параболы (1; -2)
Возьмем дополнительные точки, где х ≥−12
| х | -0,5 | 0 | 2 | 3 |
| у | 0,25 | -1 | -1 | 2 |
у=х2 + 2х + 1
Аналогично найдем вершину второй параболы: х0=-1, у0=0
Вершина второй параболы (-1;0)
Дополнительные точки при х<−0.5
| х | -2 | -0,5 |
| у | 1 | 0,25 |
Изобразим параболы в системе координат:
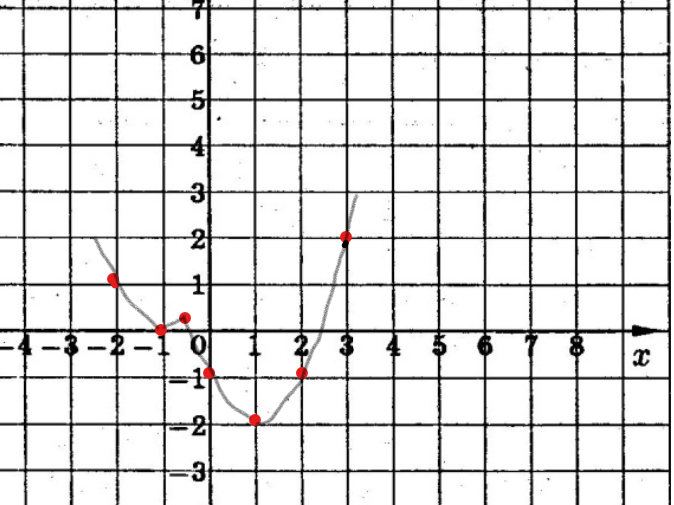
Теперь нам нужно ответить на вопрос задания: «Определите, при каких значениях m прямая у= m имеет с графиком ровно три общие точки?»
Для этого построим такие прямые (одна желтая, вторая зеленая), откуда видно, что первая прямая совпадает с осью х, т.е. у=0; вторая имеет с графиком три общие точки при у=0,25.
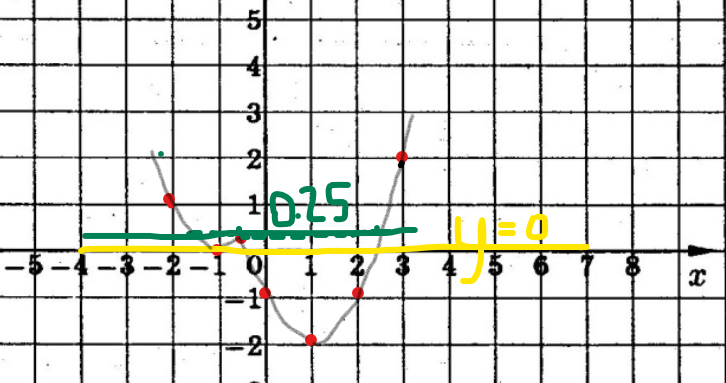
Ответ: при m равных 0; 0,25
Ответ: см. решение
Текст: Базанов Даниил, 933 👀
Подписаться
авторизуйтесь
Пожалуйста, войдите, чтобы прокомментировать
0 комментариев
Старые