Задание OM2303o
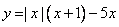
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки. В ответ запишите наибольшее число.
📜Теория для решения:
Посмотреть решение
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу функции в зависимости от знака переменной
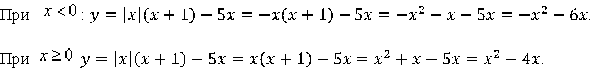
2. Определяем вид функции и находим дополнительные точки для каждого участка графика.
График при 
— часть парабола, ветви которой направлены вниз. Потому как коэффициент а=-1 – отрицательный.
Определим вершину параболы 
и 
.
Вершина находится в точке (-3; 9).
Парабола проходит еще через точки (0;0) и (0;6).
Если 
, ветви параболы направлены вверх. Найдем вершину:
, 
(2; -4).
График проходит также через точки (0;0) и (0;4).
3. Строим искомый график:
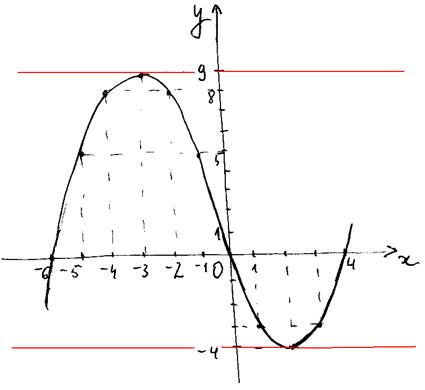
Из построения видно, что прямая y=m имеет только 2 общие точки с графиком функции в случаях, когда m=-4 или m=9. На рисунке прямые изображены красным цветом.
Ответ: 9