Задание OM2201o
📜Теория для решения:
Посмотреть решение
Алгоритм решения:
- Введем неизвестную величину: скорость третьего.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Выясняем, на какой вид движения эта задача.
- Используя условие, формулы времени или скорости, выражаем через неизвестную величину все остальные.
- Исходя из условия, составляем равенство и преобразуем его.
- Решаем уравнение.
- Определяем величины, которые еще нужно найти.
- Записываем ответ.
Решение:
1. Обозначим через x км/ч скорость третьего велосипедиста.
2. Составим таблицу их краткого условия:
| v, км/ч | t, ч | S, км | |
| 1 велосипедист | 21 | На 2 ч раньше всех | |
| 2 велосипедист | 15 | На 1 ч раньше третьего | |
| 3 велосипедист | х |
3. Задача на движение водном направлении, значит, для определения совместной скорости (сближения), необходимо из большей скорости вычитать меньшую. Наибольшая скорость была у третьего велосипедиста, потому что он догонял двух других.
4. Перед тем, как выехал третий велосипедист, первый двигался уже 2 часа. За это время он проехал 42 км, а второй проехал 15 км, поскольку был в пути 1 час. Совместная скорость третьего и второго велосипедистов равна (x-15) км/ч. так как они движутся в одном направлении. Третий велосипедист догнал второго спустя ![]() ч после своего выезда.
ч после своего выезда.
Совместная скорость третьего и первого велосипедистов равна (x-21)км/ч. Третий велосипедист догнал первого через ![]() ч после своего выезда из поселка.
ч после своего выезда из поселка.
По условию третий велосипедист догнал первого спустя 9 ч после того, как догнал второго.
5. Исходя из этого, составим равенство:
![]() ,
,
Преобразуем полученное уравнение:

6. Получили квадратное уравнение. Решим его:
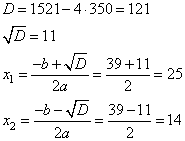
По условию скорость третьего велосипедиста была наибольшей, значит, второй корень не удовлетворяет условию. Получаем. Что решением будет x = 25 км/ч.
Ответ: 25