Задание OM2202o
📜Теория для решения:
Посмотреть решение
Алгоритм решения:
- Введем неизвестные величины: скорость третьего и время его движения.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Используя условие, формулы времени или скорости, выражаем через неизвестные величины все остальные.
- Исходя из условия, составляем равенства.
- Составляем и решаем систему уравнений.
- Определяем величины, которые еще нужно найти.
- Записываем ответ.
Решение:
1. Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догнал второго велосипедиста.
2. Составим таблицу данных условия:
| v, км/ч | t, ч | s, км | |
| 1 велосипедист | 15 | t +7 | |
| 2 велосипедист | 10 | t +1 | |
| 3 велосипедист | х | t |
3. До места встречи со вторым велосипедистом третий проехал x·t км.
Скорость второго велосипедиста 10 км/ч. В пути он находился t + 1 часов к моменту встречи с третьим велосипедистом. Тогда в момент встречи велосипедисты находились на расстоянии 10·(t + 1) км от поселка. Расстояния эти одинаковы, значит, x·t = 10·(t + 1).
Первого велосипедиста третий догонит через t + 5 ч – время, за которое он догнал первого велосипедиста после второго, тогда до места встречи с первым велосипедистом третий проехал x·(t + 5) км.
Первый велосипедист ехал со скоростью 15 км/ч и был в пути до встречи с третьим t + 7 часов, потому как выехал он на 2 часа раньше. Расстояние, которое проехал первый велосипедист, равно 15·(t + 7) км.
Получаем еще одно равенство: x·(t + 5) = 15·(t + 7)
4. Составляем систему уравнений:
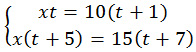
5. Решаем полученную систему, преобразовав каждое из уравнений:
![]()
Вычитаем из второго уравнение первое, получаем
5x = 5t + 95
x = t + 19
Подставляем вместо x в первое уравнение системы правую часть равенства и решаем полученное уравнение.
(t + 19)·t = 10t + 10
t2 + 19t = 10t + 10
t2 + 9t – 10 = 0
По формуле дискриминанта и корней:
D = b2 – 4ac
D = 92 — 4·1·(-10) = 81 + 40 = 121
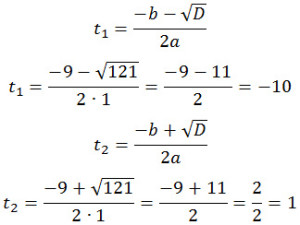
Первый ответ не может удовлетворять условию задачи, поскольку время не может иметь отрицательных значений. Следовательно,
x = t + 19 = 1 + 19 = 20
Скорость третьего велосипедиста 20 км/ч.
Ответ: 20