Задание OM2301o
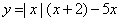
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки. В ответ запишите наибольшее число.
📜Теория для решения:
Посмотреть решение
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем функцию в зависимости от знака переменной х.
Если ![]() .
. ![]()
Если ![]()
![]()
2. График функции ![]() заданных значениях х — часть параболы, ветви которой направлены вниз.
заданных значениях х — часть параболы, ветви которой направлены вниз.
Вершина расположена в точке с координатами: ![]()
![]()
Найдем нули функции: ![]() График проходит через начало координат и точку (-2;-7).
График проходит через начало координат и точку (-2;-7).
Графиком второй функции ![]() является парабола, ветви которой направлены вверх.
является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
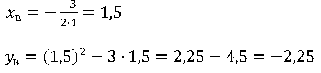
Определим нули параболы ![]()
3. Изображаем график функции на координатной плоскости:
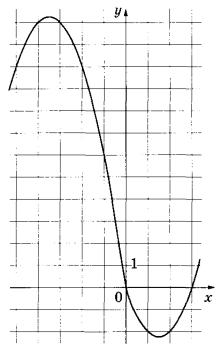
4. Из построения легко видно, что прямая y = m имеет с графиком ровно две точки, когда проходит через вершину одной из парабол, образующих график данной функции.
Значит, две общие точки функция и прямая имеют при m = -2,25 или m = 12,25.
Ответ: 12,25
У меня вопрос : » Куда исчез » минус» перед х в квадрате при нахождении координаты параболы у нулевое -х2 — 7х?
Смотреть далее решение! В остальном, большое спасибо!