Задание OM2501o • СПАДИЛО

Окружности с центрами в точках I и J пересекаются в точках А и В, причём точки I и J лежат по одну сторону от прямой АВ. Докажите, что прямые АВ и IJ перпендикулярны.

📜Теория для решения:

Посмотреть решение

Алгоритм решения:

Делаем чертеж.
Определяем место расположения точек I и J.
Используем свойство серединного перпендикуляра.
Делаем вывод.

Решение:

1. Делаем чертеж, согласно условия:

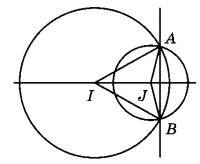
2. Определяем место расположения точек I и J:

Точка I равноудалена от точек A и B. Аналогично, точка J равноудалена от концов отрезка AB.

3. По свойству геометрического места точек, равноудаленных от концов отрезка, эти точки расположены на серединном перпендикуляре к отрезку AB.

А если две точки I и J лежат на серединном перпендикуляре, прямая IJ совпадает с ним. Следовательно, прямые IJ и АВ перпендикулярны.

Ответ: доказано

Текст: Базанов Даниил, 604 👀