Задание OM2502o • СПАДИЛО

Окружности с центрами в точках Е и F пересекаются в точках С и D, причём точки Е и F лежат по одну сторону от прямой CD. Докажите, что прямые CD и EF перпендикулярны.

📜Теория для решения:

Посмотреть решение

Алгоритм решения:

Делаем чертеж по условию задачи.
Рассмотрим треугольники CEF и DEF и установим их равенство.
Воспользуемся свойством равных фигур для определения вида треугольника CED.
Используем свойство равнобедренного треугольника и делаем вывод.

Решение:

1. Делаем чертеж по условию задачи:

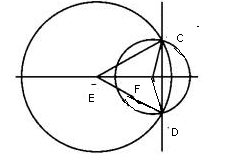
Безымянный.bmp

2. Рассмотрим треугольники CEF и DEF и установим их равенство:

У них CE=DE, как радиусы окружности с центром в точке Е,

Аналогично, CF = DF, как радиусы окружности с центром в точке F.

EF – общая сторона.

Значит, данные треугольники равны.

Тогда по свойству равных фигур .

Рассмотрим треугольник CED. У него CE=DE, поскольку это соответствующие стороны равных фигур. Значит, треугольник равнобедренный.

EF – биссектриса угла E. следовательно, EF – высота по свойству равнобедренного треугольника. Отсюда следует, что .

Ответ: доказано

Текст: Базанов Даниил, 585 👀