Задание OM2505o • СПАДИЛО

В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC= ED. Докажите, что данный параллелограмм — прямоугольник.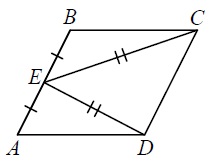

📜Теория для решения:

Посмотреть решение

Рассмотрим треугольники BEC и AED. BE = EA, так как E — середина стороны AB по условию. EC= ED по условию, а BC = AD по свойству параллелограмма (противолежащие стороны равны). Таким образом, BE = EA, EC= ED, BC = AD. Следовательно, треугольники BEC и AED равны по трём сторонам.

В равных треугольниках — равные элементы. Значит, углы CBE и DAE равны. Так как их сумма равна 180° по свойству параллелограмма , то углы равны 90° (180 / 2 = 90 ) .

Следовательно, данный параллелограмм — прямоугольник.

Ответ: доказано

Текст: Базанов Даниил, 1.2k 👀