Задание OM2504o
ОГЭ▿высокий уровень сложности▿другое(архив)
В выпуклом четырёхугольнике ABCD углы ВСА и BDA равны. Докажите, что углы ABD и ACD также равны.
📜Теория для решения:
2. Рассматриваем треугольники BOC и AOD.У них:
углы ВСА и BDA равны по условию задачи,
углы BOC и AOD равны как вертикальные.
Значит, треугольники BOC и AOD подобны по двум углам.
3. Для подобных треугольников BOC и AOD записываем соотношение соответствующих сторон:
4. Рассматриваем треугольники AOB и DOC. У них:
углы AOB и DOC равны как вертикальные.
Следовательно, данные треугольники подобны.
📜Теория для решения:
Посмотреть решение
Алгоритм решения:
- Выполняем рисунок по условию задачи.
- Устанавливаем подобие треугольников BOC и AOD.
- Записываем соотношение для сторон.
- Устанавливаем подобие треугольников AOB и DOC.
- Делаем вывод.
Решение:
1. Выполняем чертеж по условию задачи:
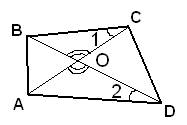
2. Рассматриваем треугольники BOC и AOD.У них:
углы ВСА и BDA равны по условию задачи,
углы BOC и AOD равны как вертикальные.
Значит, треугольники BOC и AOD подобны по двум углам.
3. Для подобных треугольников BOC и AOD записываем соотношение соответствующих сторон:
4. Рассматриваем треугольники AOB и DOC. У них:
углы AOB и DOC равны как вертикальные.
Следовательно, данные треугольники подобны.
По свойству подобных фигур соответствующие углы в треугольниках равны. Значит, 
, а поскольку эти углы совпадают с углами ABD и ACD , то 
.
Даниил Романович | Просмотров: 388