Задание OM1702o • СПАДИЛО

Касательные в точках A и B к окружности с центром O пересекаются под углом 2º. Найдите угол ABO. Ответ дайте в градусах.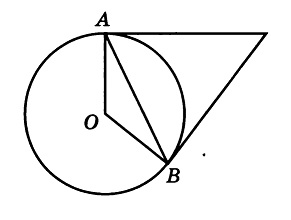 решение 10 задания огэ по математике

📜Теория для решения:

Посмотреть решение

Во-первых, касательные равны между собой по длине, а значит треугольник с основанием AB равнобедренный. Угол при вершине этого треугольника равен 2 градуса по условию, значит углы при основании равны:

(180 — 2) / 2 = 89°

Во-вторых, касательные перпендикулярны радиусу, то есть угол между ними и радиусом равен 90 градусов.

Заметим, что угол ABO, который необходимо найти, является частью угла между касательной и радиусом, а именно за вычетом угла, который мы нашли в первом пункте. Значит, этот угол равен:

90 — 89 = 1°

Ответ: 1

Текст: Базанов Даниил, 870 👀