Задание OM2401o
ОГЭ▿высокий уровень сложности▿другое(архив)
Углы В и С треугольника ABC равны соответственно 71° и 79°. Найдите ВС, если радиус окружности, описанной около треугольника ABC, равен 8.
📜Теория для решения:
2. Определим угол А: ∠А=1800 —710—790 = 300.
3. Пусть R — радиус описанной окружности, тогда по следствию из теоремы синусов получаем:
4. Тогда, при подстановке в равенство полученных данных, получаем: ВС равно произведению сторон АВ и АС на синус угла А, который равен 300. Следовательно ВС=2∙8∙0,5=8.Ответ: 8
📜Теория для решения:
Посмотреть решение
Алгоритм решения:
- Делаем чертеж по условию задания.
- Находим угол А в данном треугольнике.
- Используем следствие из теоремы синусов для треугольника АВС
- Определяем ВС.
- Записываем ответ.
Решение:
1. Делаем чертеж, удовлетворяющий условию задачи.
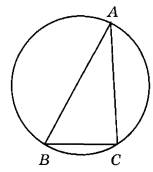
2. Определим угол А: ∠А=1800 —710—790 = 300.
3. Пусть R — радиус описанной окружности, тогда по следствию из теоремы синусов получаем:
4. Тогда, при подстановке в равенство полученных данных, получаем: ВС равно произведению сторон АВ и АС на синус угла А, который равен 300. Следовательно ВС=2∙8∙0,5=8.Ответ: 8
Даниил Романович | Просмотров: 387