Задание OM2405o

Решение:

1. Выполняем соответствующий чертеж: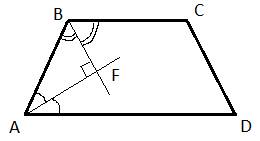

2. Трапеция ABCD имеет основаниями стороны ВС и AD, значит, они параллельны. Тогда в ней внутренние односторонние при пересечении прямых, которые содержат эти основания, секущей АВ. Следовательно, они удовлетворяют равенству: .

3. По построению, заданному условием задачи AF и BF являются биссектрисы данных углов. Тогда в треугольнике ABF

Отсюда получаем:

Таким образом, треугольник AFB прямоугольный, а сторона AB – его гипотенуза.

4. Используем теорему Пифагора: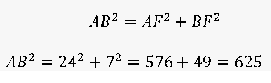

Отсюда АВ=25.