Задание OM2406o
ОГЭ▿высокий уровень сложности▿другое(архив)
Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF = 20, BF = 15.
📜Теория для решения:
2. Рассмотрим трапецию ABCD. В ней 
как основания. Углы А и В составляют в сумме 1800, как углы при основаниях. Отсюда следует, что 
как соседние при двух основаниях. По условию лучи AF и BF – биссектрисы этих углов, тогда их сумма
📜Теория для решения:
Посмотреть решение
Алгоритм решения:
- Делаем чертеж.
- Рассматриваем углы трапеции и проведенные биссектрисы.
- Определяем вид треугольника AFB.
- Находим длину АВ.
- Записываем ответ.
Решение:
1. Выполняем рисунок, соответствующий данному условию.
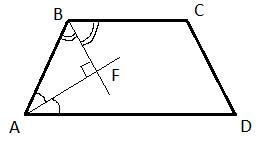
2. Рассмотрим трапецию ABCD. В ней как основания. Углы А и В составляют в сумме 1800, как углы при основаниях. Отсюда следует, что как соседние при двух основаниях. По условию лучи AF и BF – биссектрисы этих углов, тогда их сумма
3. Рассматриваем треугольник ABF. В нем угол 
по свойству углов треугольника, т.е. построенный треугольник AFB – прямоугольный. И гипотенузой в нем является сторона AB.
Следовательно, АВ=25.
Ответ: 25
Даниил Романович | Просмотров: 526