Задание EF22682

Алгоритм решения

Решение

Запишем исходные данные:

Сделаем рисунок. Так как препятствие квадратное, оно располагается параллельно полу, а его центр лежит на одной вертикали с точечным источником света, можем построить рисунок, наблюдая картину с одной стороны квадратного препятствия. В этом случае OE соответствует высоте потолка, EB — расстоянию от пола до препятствия, а AC — стороне квадратного препятствия. При этом тень будет иметь форму квадрата. Поэтому для нахождения ее площади достаточно найти сторону этого квадрата — DF.

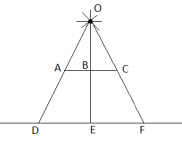
Треугольники OBC и OEF являются подобными по трем углам. Угол O у них общий. Углы B и E — прямые (так как они образованы при пересечении вертикалью двух параллельных плоскостей). А углы C и F равны как углы при параллельных прямых и секущей.

Следовательно, OB относится к OE так же, как BC относится к EF. Причем EF — половина стороны квадрата тени, поскольку треугольник DOF — равнобедренный. Это следует из того, что перпендикуляр, проведенный к основанию равнобедренного треугольника, одновременно является его биссектрисой и медианой. Следовательно, отрезок OE делит на 2 равные части DF.

Отсюда:

$\frac{OB}{OE}=\frac{BC}{EF}$

Умножим числитель и знаменатель дроби в правой части уравнения и получим:

$\frac{OB}{OE}=\frac{2BC}{2EF}=\frac{AC}{DF}$

Причем OB можно вычислить как разность высоты потолка и расстояния от препятствия до пола:

$OB=OE-BE$

Получаем:

$DF=\frac{OE·AC}{H-h}=\frac{aH}{H-h}=\frac{2·4}{4-2}=4\left(м\right)$

Это сторона квадрата тени. Чтобы найти площадь тени, нужно возвести эту величину в квадрат:

$S={DF}^2=4^2=16\left({м}^2\right)$