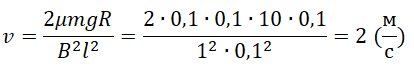Задание EF18860 • СПАДИЛО

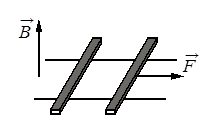По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой m = 100 г и сопротивлением R = 0,1 Ом каждый. Расстояние между рельсами l = 10 см, а коэффициент трения между стержнями и рельсами μ = 0,1 Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией B = 1 Тл (см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь. Ответ записать в системе СИ.

📜Теория для решения: Закон электромагнитной индукции

Посмотреть решение

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Записать закон электромагнитной индукции для двигающихся стержней.

3.Выполнить решение задачи в общем виде.

4.Подставить неизвестные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса стержней:

m_{1} = m_{2} = m = 100

г.

• Сопротивление стержней:

R_{1} = R_{2} = R = 0, 1

Ом.

• Расстояние между рельсами: l = 10 см.

• Коэффициент трения между стержнями и рельсами: μ = 0,1.

• Модуль вектора магнитной индукции магнитного поля: B = 1 Тл.

• Угол между вектором магнитной индукцией и вектором скорости стержней: α = 90 градусов (синус прямого угла равен «1»).

100 г = 0,1 кг

10 см = 0,1 м

Когда под действием некой силы начинается двигаться первый стержень, магнитный поток, пронизывающий контур, образованные проводящими рельсами и двумя стержнями, меняется. Это приводит к возникновению в этом контуре электродвижущей силы, которую можно определить с помощью закона электромагнитной индукции для двигающихся стержней:

$ε_{i} = v B l sin . α$

Причем v — это разность скоростей стержней (v₂ – v₁), которая характеризует скорость изменения площади проводящего контура.

Индукционный ток, возникающей в этом контуре, можно выразить, используя закон Ома:

$ε_{i} = I R_{к}$

где $R_{к}$ — сопротивление контура. Так как стержни соединяются последовательно, и их сопротивления равны R, а сопротивление рельсов ничтожно мало, сопротивление контура равно:

$R_{к} = 2 R$

Отсюда закон Ома принимает вид:

$ε_{i} = 2 I R$

Тогда ток в контуре равен:

$I = \frac{ε_{i}}{2 R} = \frac{v B l sin . α}{2 R}$

С одной стороны на стержни действует сила Ампера, с другой — сила трения, возникающего между ними и рельсами. Так как стержни движутся равномерно, равнодействующая сил, приложенных к ним, равна нулю. Следовательно, сила трения и сила Ампера компенсируют друг друга (их модули равны):

$F_{т р} = F_{А}$

$μ m g = B I l sin . α$

Подставим сюда выражение, полученное для силы тока в контуре:

$μ m g = B \frac{v B l sin . α}{2 R} l sin . α = \frac{{v B}^{2} l^{2} {sin}^{2} . α}{2 R}$

Отсюда скорость равна:

$v = \frac{2 μ m g R}{B^{2} l^{2} {sin}^{2} . α}$

Так как синус угла равен «1»:

Ответ: 2

Текст: Алиса Никитина, 969 👀