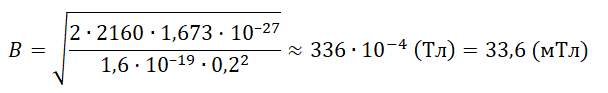Задание EF17621

Алгоритм решения

Решение

Запишем исходные данные:

20 см = 0,2 м

Сила Лоренца определяется формулой:

$F_{Л}=\left|q\right|vB\sin .\alpha$

По условию задачи протон движется перпендикулярно вектору магнитной индукции. Поэтому синус угла между вектором скорости и вектором магнитной индукции будет равен 1. А протон имеет положительный заряд. Тогда:

$F_{Л}=qvB$

Сила Лоренца сообщает протону центростремительное ускорение, равное:

$a=\frac{v^2}{R}$

Применим второй закон Ньютона:

$F=ma$

$qvB=\frac{m{v}^2}{R}$

Отсюда модуль вектора магнитной индукции равен:

$B=\frac{m{v}^2}{qvR}=\frac{mv}{qR}$

Энергия заряда, движущегося в электрическом поле, определяется формулой:

$W=qU$

Но энергию заряда также можно выразить как кинетическую энергию движения:

$W=E_{к}=\frac{m{v}^2}{2}$

Приравняем правые части выражений и получим:

$qU=\frac{m{v}^2}{2}$

Отсюда ускорение протона равно:

$v=\sqrt{\frac{2qU}{m}}$

Конечная формула для определения модуля вектора магнитной индукции:

$B=\frac{mv}{qR}=\frac{m}{qR}\sqrt{\frac{2qU}{m}}=\sqrt{\frac{2Um}{q{R}^2}}$