Задание OM2102o
ОГЭ▿высокий уровень сложности▿другое(архив)
Решите уравнение и запишите в ответ наибольший из корней: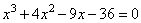
📜Теория для решения:
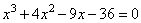
📜Теория для решения:
Посмотреть решение
5. После деления получаем квадратный трехчлен:
Ответ: 3
Текст: Базанов Даниил, 951 👀
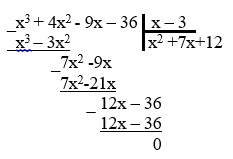
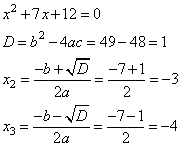
Данное уравнение решается быстрее разложением на множители!!!