Задание OM2103o
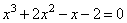
📜Теория для решения:
Посмотреть решение
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
1. Перед нами кубическое уравнение общего вида.
2. Найдем делители свободного члена уравнения. Это числа: 1; -1 и 2; -2.
3. Определим один из корней кубического уравнения среди делителей свободного члена .Для этого подставим каждый из этих делителей вместо x и проверим, какой их них является корнем:
— для x=1: ![]() — подходит это и есть один из корней.
— подходит это и есть один из корней.
4. Теперь выполним деление кубического многочлена на x-1, воспользовавшись схемой Горнера, имеем:
| 1 | 2 | -1 | -2 | |
| 1 | 1 | 3 | 2 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
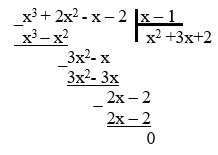
5. Получаем квадратный трехчлен
x2 +3x+2
6. Составим и решим квадратное уравнение для вычисления оставшихся двух корней. Для этого воспользуемся формулами корней квадратного уравнения и дискриминантом.
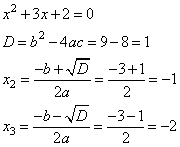
7. Получили три корня -2; -1; 1.
Ответ: -2
здравствуйте, в ведь можно же решить способом легче
1.вынести общие множители
х2(х+2)-1(х+2)=0
(х2-1)(х+2)=0
х=+-1 и х=-2
и тогда меньший корень х=-2