Задание OM2106o
ОГЭ▿высокий уровень сложности▿другое(архив)
Решите систему уравнений. В ответ запишите пару чисел сумма которых наибольшая в порядке возрастания. Например, 47, если один из корней равен 4, а другой 7.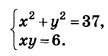
📜Теория для решения:
Из (2) выражаем у через х:
Полученное выражение для у подставляем в (1):
Выполним преобразования:
Выполним замену: х2= , а≠0 .
Получим:
Корни системы: (–1; –6), (1; 6), (–6; –1), (6; 1)Ответ: 16
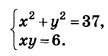
📜Теория для решения:
Посмотреть решение
Алгоритм решения:
- Из 2-го уравнения выражаем у через х.
- Подставляем полученное выражение для у в 1-е уравнение.
- В полученном уравнении с одной переменной (х) выполняем тождественные преобразования. Приводим его к квадратичному виду.
- Выполняем замену х2 на а. Решаем полученное квадратное уравнение.
- Возвращаемся от а к х. Находим все значения (корни) для х.
- Определяем соответствующие им значения для у.
- Фиксируем в ответе пары соответствующих корней.
Решение:
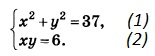
Из (2) выражаем у через х:
Полученное выражение для у подставляем в (1):
Выполним преобразования:
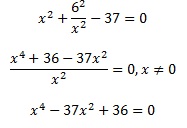
Выполним замену: х2= , а≠0 .
Получим:
а2–37а+36=0
По теореме Виета а1=1, а2=36 Отсюда имеем:х2=1 → х=±1 → х1=–1, х2=1
х2=36 → х=±6 → х3=–6, х4=6
Теперь возвращаемся к уравнению, в котором у выражено через х. И вычисляем соответствующие значения для у:
Корни системы: (–1; –6), (1; 6), (–6; –1), (6; 1)Ответ: 16
Даниил Романович | Просмотров: 501
А ещё можно x²+y² представить в виде (x+y)²-2xy
Тогда первое уравнение будет выглядеть так
(x+y)²=37+12
(x+y)²=49
И получаем что
x+y=7
x+y=-7
Выражаем y, подставляем и находим. Ответ получается точно такой же