Задание OM2005
ОГЭ▿высокий уровень сложности▿другое()
Решить неравенство(х−5)2<√7(х−5)
📜Теория для решения: Квадратные неравенства с одной переменной
Итак, видно, что необходимый интервал от 5 до (5+√7)
Ответ: (5;5+√7)Ответ: см. решение
📜Теория для решения: Квадратные неравенства с одной переменной
Посмотреть решение
Для того чтобы начать решать неравенство, мы должны понимать, интервал каких чисел будем находить – положительных или отрицательных. Для этого перенесем выражение из правой части в левую, изменяя знак на противоположный, и справа от знака «меньше» образуется нуль:
(х−5)2−√7(х−5)<0 Теперь вынесем за скобки общий множитель (х-5), получим: (х−5)(х−5−√7)<0 Найдем нули функции, приравнивая каждый множитель к нулю: х−5=0, откуда х=5 х−5−√7=0, откуда: х=5+√7 Отметим эти числа на числовом луче и найдем интервал отрицательных чисел:
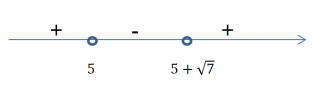
Итак, видно, что необходимый интервал от 5 до (5+√7)
Ответ: (5;5+√7)Ответ: см. решение
Даниил Романович | Просмотров: 1k