Задание Статика 2
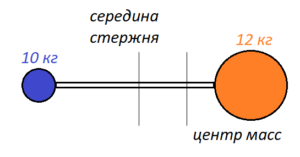Два однородных шара массами 10 и 12 кг с радиусами 4 и 6 см соединены посредством однородного стержня массой 2 кг и длиной 10 см. Центры шаров лежат на продолжении оси стержня. Найти расстояние в см от центра тяжести этой системы до оси, проходящей через середину стержня. 📜Теория для решения: Момент силы и правило моментов Правило моментов при решении задач Давление твердого тела
Посмотреть решение
Алгоритм решения:
Решение:
Запишем исходные данные:
СИ не соответствует только мера длины. Но так как все длины приведены в сантиметрах, мы можем условиться использовать их. Но тогда все полученные результаты в вычислениях длин будут представлены в сантиметрах — именно в них по условию задачи нужно определить расстояние от центра тяжести этой системы до оси, проходящей через середину стержня.
Так как шары однородные, можем считать, что центры их масс находятся в центре шаров. По этой же причине все центры масс лежат на одной прямой. Всю систему тел можем считать твердым телом с осью вращения в точке, которая лежит на расстоянии x от оси, проходящей через середину стержня.
Чтобы найти искомую величину, вспомним, что система будет находиться в равновесии, если ось вращения будет проходить через ее центр масс. А условие равновесия относительно вращения твёрдого тела на оси — равенство нулю суммы моментов сил, приложенных к телу, относительно этой оси. Сделаем рисунок и запишем это условие равновесия, учитывая следующее:
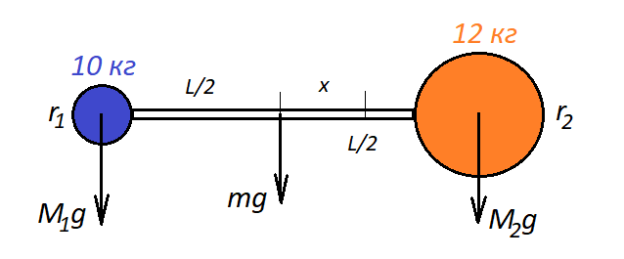
Учитывая сказанное выше, условие равновесия системы принимает вид:
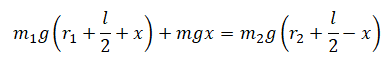
Или:
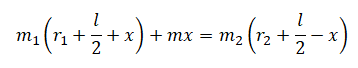
Все величины, кроме искомой, являются известными. Можно было бы упросить выражение, но в условиях данной задачи будет проще сразу подставить известные величины, а затем произвести необходимые вычисления:
.
.
.
.
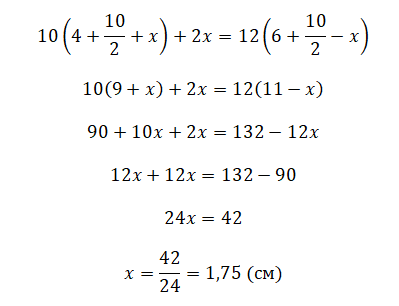
Ответ: 1,75