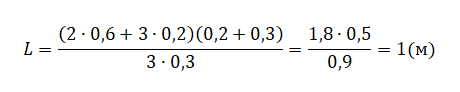Задание Статика 4
Два небольших шара массами m1 = 0,2 кг и m2 = 0,3 кг закреплены на концах невесомого стержня AB, расположенного горизонтально на опорах C и D (см. рис.). Расстояние между опорами l = 0,6 м, а расстояние AC равно 0,2 м. Чему равна длина стержня L, если сила давления стержня на опору D в 2 раза больше, чем на опору C? Сделайте рисунок с указанием внешних сил, действующих на систему тел «стержень — шары». 📜Теория для решения: Момент силы и правило моментов Правило моментов при решении задач Давление твердого тела
Посмотреть решение
Алгоритм решения:
Решение:
Запишем исходные данные:
Систему отсчёта, связанную с Землёй, будем считать инерциальной (ИСО). Стержень невесомый, сила трения отсутствует. Потому можем сделать рисунок и указать на нем силы следующим образом:
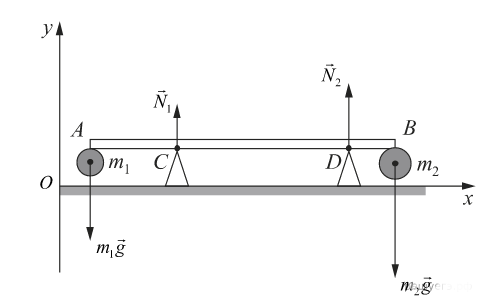
К опорам C и D приложены только силы нормальной реакции опоры 1 и 2. Следовательно, модули сил давления будут соответственно равны силам нормальной реакции опоры 1 и 2:
Отсюда отношение второй силы нормальной реакции опоры ко второй равно:
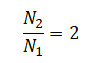
Или:
Так как центр масс не движется вдоль оси Оу, можем записать следующее условие равновесия системы тел:
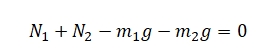
Так как нет вращения вокруг оси, которая проходит через точку А перпендикулярно рисунку:
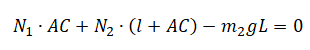
Подставим силу реакции 2, выраженную через силу реакции 1:
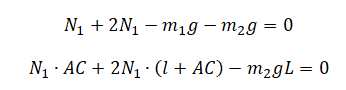
Преобразуем уравнения:
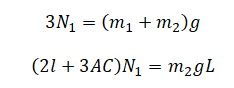
Из верхнего уравнения выразим силу реакции 1 и подставим выражение в нижнее уравнение:
Выразим длину стержня и сделаем необходимые преобразования:
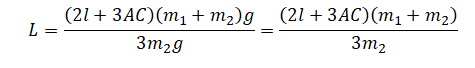
Вычислим:
