Задание OM2003
📜Теория для решения: Квадратные неравенства с одной переменной
Посмотреть решение
Имеем дробное неравенство, где решать надо будет только знаменатель. Но для этого посмотрим, что решением неравенства являются числа, которые больше или равны нулю. Для этого наш знаменатель должен быть отрицательным числом, так как числитель – число тоже отрицательное, а при делении двух отрицательных чисел получим число положительное. Далее, знаменатель не должен быть равен нулю, так как на нуль делить нельзя. Следовательно, начнем решение с того, что выпишем знаменатель, который должен быть отрицательным числом:
(х – 2)2 – 3<0
У нас получилось квадратное неравенство, которое мы и должны решать. Начнем с раскрытия скобок по формуле сокращенного умножения и приведения подобных слагаемых:
х2 – 4х+4 – 3 <0
х2 – 4х+1 <0
Получим квадратное неравенство, для которого надо найти интервал отрицательных чисел (<0)
Для этого найдем нули функции, решая с помощью дискриминанта:
Д=(-4)2 — 4∙1∙1=16-4=12
х1=4− √122=2(2−√3)2=2−√3
Знаем, что х2 будет отличаться только знаком, получим, что х2=2+√3
Теперь отмечаем числа на числовом луче и показываем интервалы справа налево путем чередования знаков. Видим, что наш интервал отрицательных чисел – от точки (2−√3) до точки (2+√3).
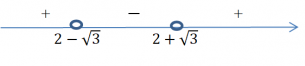
Ответ: (2−√3 ; 2+√3)