Задание Статика 3 • СПАДИЛО

Алюминиевая спица длиной 25 см и площадью поперечного сечения 0,1 см²подвешена на нити за верхний конец. Нижний конец опирается на горизонтальное дно сосуда, в который налита вода. Длина погруженной в воду части спицы равна 10 см. Найти силу, с которой спица давит на дно сосуда, если известно, что нить расположена вертикально. Плотность алюминия равна 2,7 г/см³. Плотность воды равна 1 г/см³. Ускорение свободного падения считать равным 10 м/с². Считать, что трение отсутствует. Ответ запишите в мН с точностью до сотых.

📜Теория для решения: Момент силы и правило моментов Правило моментов при решении задач Давление твердого тела

Посмотреть решение

Алгоритм решения:

1.Записать исходные данные и при необходимости перевести единицы измерения величин в СИ.

2.Определить физические законы, которые можно применять для решения данной задачи. Обосновать возможность их использования.

3.Сделать поясняющий рисунок с указанием всех сил.

4.Применить описанные законы в условиях данной задачи. Путем преобразования формул вывести искомую величину.

5.Подставить известные значения и произвести вычисления.

Решение:

Запишем исходные данные:

• Длина алюминиевой спицы: L = 25 см.

• Длина части спицы, погруженной в воду: l = 10 см.

• Площадь поперечного сечения спицы: S = 0,1 см².

• Плотность алюминия: ρ_ал = 2,7 г/см³.

• Плотность воды: ρ_в = 1 г/см³.

• Ускорение свободного падения: g = 10 м/с².

Чтобы все единицы были соразмерны, переведем их в СИ:

L = 25 см = 0,25 м

l = 10 см = 0,1 м

S = 0,1 см² = 10^–5 м²

ρ_ал = 2,7 г/см³=2700 кг/м^3.

ρ_в = = 1 г/см³=1000 кг/м³

Систему отсчёта, связанную с Землёй, будем считать инерциальной (ИСО). По условию задачи спица однородная. Нить будем считать невесомой. Система тел находится в состоянии равновесия. Поэтому будем применять правило моментов сил.

Сделаем поясняющий рисунок, учитывая следующее:

• Сила тяжести стержня прикладывается к геометрическому центру спицы (потому что она однородная).

• Так как спица однородная, сила Архимеда, действующая на нее, прикладывается к центру погруженной части спицы.

• Сила натяжения нити и сила нормальной реакции опоры прикладываются соответственно к верхнему и нижнему концу спицы.

• Сила трения по условию задачи отсутствует.

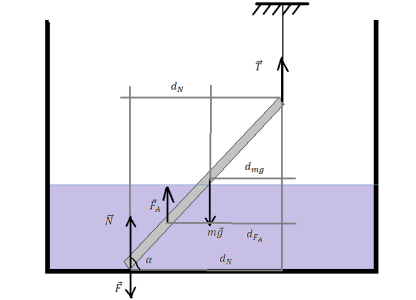
Так как сила трения отсутствует, можем модуль искомой силы F принять за модуль силы нормальной реакции опоры. Следовательно, вся задача сводится к вычислению N.

Будем рассматривать равновесие системы относительно верхнего конца спицы. К этой точке приложена сила натяжения нити. Поэтому ее плечо равно 0. Следовательно, момент силы натяжения нити равен 0.

Плечо силы нормальной реакции опоры будет равно произведению длины спицы на косинус угла α:

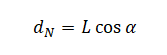
Плечо силы Архимеда будет равно произведению косинуса угла α на разность длины спицы и половины длины погруженной части спицы:

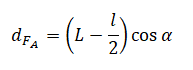
Плечо силы тяжести будет равно половине длины спицы на косинус угла α:

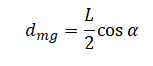
Учитывая направление сил относительно вертикали, составляем условие равновесия:

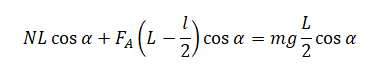
Поделим на косинус и получим:

Сила Архимеда равна произведению плотности жидкости на ускорение свободного падения и объем погруженной части тела. Этот объем равен произведения площади поперечного сечения спицы на длину погруженной части:

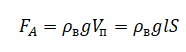
Сила тяжести равна произведения массы на ускорение свободного падения. А массу можем найти как произведение плотности алюминия, из которого сделана спица, на объем спицы. А объем равен произведению длины на площадь поперечного сечения:

Следовательно, условие равновесия принимает вид:

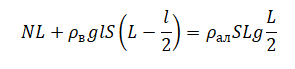
Выразим искомую величину:

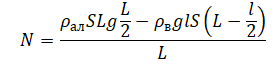
Считаем:

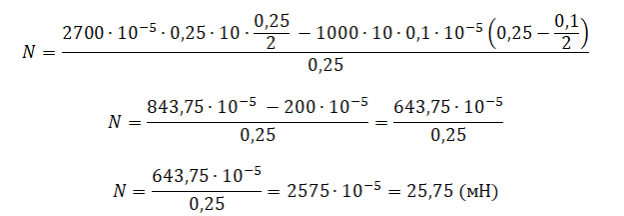
Следовательно, спица давит на дно с силой 25,75 мН.

Ответ: 25,75

Текст: Алиса Никитина, 81 👀